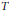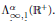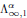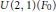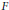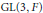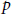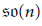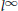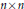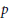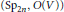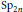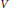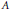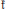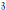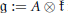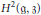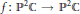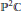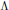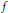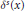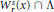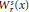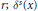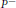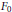Contents
Research Article
H∞ Functional Calculus and Mikhlin-Type Multiplier Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1010-1027
-
- Article
-
- You have access
- Export citation
Types, paquets et changement de base : l’exemple de U(2, 1)(F 0). I. Types simples maximaux et paquets singletons
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 790-821
-
- Article
-
- You have access
- Export citation
Nilpotent Conjugacy Classes in
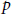 $p$ -adic Lie Algebras: The Odd Orthogonal Case
$p$ -adic Lie Algebras: The Odd Orthogonal Case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 88-108
-
- Article
-
- You have access
- Export citation
Transitive Factorizations in the Hyperoctahedral Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-312
-
- Article
-
- You have access
- Export citation
Lifting n-Dimensional Galois Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1028-1049
-
- Article
-
- You have access
- Export citation
Remarks on Littlewood–Paley Analysis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1283-1305
-
- Article
-
- You have access
- Export citation
Maximum Principles for Subharmonic Functions Via Local Semi-Dirichlet Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 822-874
-
- Article
-
- You have access
- Export citation
Affine Lines on Affine Surfaces and the Makar–Limanov Invariant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-139
-
- Article
-
- You have access
- Export citation
Polarization of Separating Invariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 556-571
-
- Article
-
- You have access
- Export citation
Asymptotic Properties for Increments of
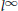 ${{l}^{\infty }}$ -Valued Gaussian Random Fields
${{l}^{\infty }}$ -Valued Gaussian Random Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-333
-
- Article
-
- You have access
- Export citation
Adjacency Preserving Maps on Hermitian Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1066
-
- Article
-
- You have access
- Export citation
Low-Pass Filters and Scaling Functions for Multivariable Wavelets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 334-347
-
- Article
-
- You have access
- Export citation
On the Geometry of
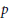 $p$ -Typical Covers in Characteristic
$p$ -Typical Covers in Characteristic 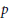 $p$
$p$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-163
-
- Article
-
- You have access
- Export citation
Theta Lifts of Tempered Representations for Dual Pairs (Sp2n ,O(V))
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1306-1335
-
- Article
-
- You have access
- Export citation
A Characterization of the Quantum Cohomology Ring of G/B and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 875-891
-
- Article
-
- You have access
- Export citation
Non-Selfadjoint Perturbations of Selfadjoint Operators in Two Dimensions IIIa. One Branching Point
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-657
-
- Article
-
- You have access
- Export citation
The Second Cohomology of Current Algebras of General Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 892-922
-
- Article
-
- You have access
- Export citation
Moving Frames for Lie Pseudo–Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1336-1386
-
- Article
-
- You have access
- Export citation
Inverse Pressure Estimates and the Independence of Stable Dimension for Non-Invertible Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-684
-
- Article
-
- You have access
- Export citation
On Types for Unramified p-Adic Unitary Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1107
-
- Article
-
- You have access
- Export citation