Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Neeb, Karl-Hermann
and
Wockel, Christoph
2009.
Central extensions of groups of sections.
Annals of Global Analysis and Geometry,
Vol. 36,
Issue. 4,
p.
381.
Dzhumadil'daev, Askar
and
Zusmanovich, Pasha
2010.
Commutative 2-cocycles on Lie algebras.
Journal of Algebra,
Vol. 324,
Issue. 4,
p.
732.
Neeb, Karl-Hermann
2011.
Developments and Trends in Infinite-Dimensional Lie Theory.
Vol. 288,
Issue. ,
p.
281.
Remm, Elisabeth
and
Goze, Michel
2014.
Algebra, Geometry and Mathematical Physics.
Vol. 85,
Issue. ,
p.
247.
Wang, Yan
Pei, Yufeng
and
Deng, Shaoqiang
2014.
Leibniz central extensions of Lie superalgebras.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 08,
p.
1450052.
Gao, Shoulan
Liu, Dong
and
Pei, Yufeng
2016.
Structure of The Planar Galilean Conformal Algebra.
Reports on Mathematical Physics,
Vol. 78,
Issue. 1,
p.
107.
Pianzola, Arturo
Prelat, Daniel
and
Sepp, Claudia
2017.
Standard cocycles: Variations on themes of C. Kassel’s and R. Wilson’s.
Forum Mathematicum,
Vol. 29,
Issue. 6,
p.
1441.
Cornulier, Yves
and
Tessera, Romain
2017.
Geometric presentations of Lie groups and their Dehn functions.
Publications mathématiques de l'IHÉS,
Vol. 125,
Issue. 1,
p.
79.
Chang, Zhihua
Cheng, Jin
and
Wang, Yongjie
2018.
Second homology of generalized periplectic Lie superalgebras.
Linear Algebra and its Applications,
Vol. 546,
Issue. ,
p.
122.
Neeb, Karl-Hermann
and
Yousofzadeh, Malihe
2018.
Current superalgebras and unitary representations.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 10,
p.
3303.
Zusmanovich, Pasha
2021.
Invariants of Lie Algebras Extended Over Commutative Algebras Without Unit.
Journal of Nonlinear Mathematical Physics,
Vol. 17,
Issue. Supplement 1,
p.
87.
Wagemann, Friedrich
2023.
Cohomology of Leibniz Algebras.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 125,
Issue. 4,
p.
239.
Ludewig, Matthias
and
Waldorf, Konrad
2024.
Lie 2-groups from loop group extensions.
Journal of Homotopy and Related Structures,
Vol. 19,
Issue. 4,
p.
597.
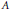 $A$ be a unital commutative associative algebra over a field of characteristic zero,
$A$ be a unital commutative associative algebra over a field of characteristic zero, 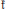 $\mathfrak{k}$ a Lie algebra, and
$\mathfrak{k}$ a Lie algebra, and 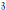 $\mathfrak{z}$ a vector space, considered as a trivial module of the Lie algebra
$\mathfrak{z}$ a vector space, considered as a trivial module of the Lie algebra 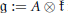 $\mathfrak{g}:=A\otimes \mathfrak{k}$. In this paper, we give a description of the cohomology space
$\mathfrak{g}:=A\otimes \mathfrak{k}$. In this paper, we give a description of the cohomology space 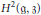 ${{H}^{2}}(\mathfrak{g},\mathfrak{z})$ in terms of easily accessible data associated with
${{H}^{2}}(\mathfrak{g},\mathfrak{z})$ in terms of easily accessible data associated with 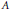 $A$ and
$A$ and 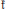 $\mathfrak{k}$. We also discuss the topological situation, where
$\mathfrak{k}$. We also discuss the topological situation, where 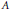 $A$ and
$A$ and 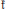 $\mathfrak{k}$ are locally convex algebras.
$\mathfrak{k}$ are locally convex algebras.