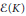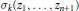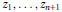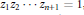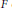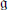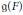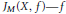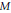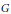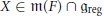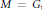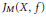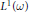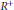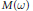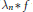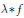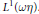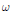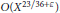Contents
Research Article
Spaces of Whitney Functions on Cantor-Type Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-238
-
- Article
-
- You have access
- Export citation
Elementary Symmetric Polynomials in Numbers of Modulus 1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-262
-
- Article
-
- You have access
- Export citation
Intégrales orbitales pondérées sur les algèbres de Lie : le cas p-adique
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-302
-
- Article
-
- You have access
- Export citation
Convergence Factors and Compactness in Weighted Convolution Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-323
-
- Article
-
- You have access
- Export citation
Parametric Representation of Univalent Mappings in Several Complex Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 324-351
-
- Article
-
- You have access
- Export citation
On Connected Components of Shimura Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 352-395
-
- Article
-
- You have access
- Export citation
Framed Stratified Sets in Morse Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 396-416
-
- Article
-
- You have access
- Export citation
Slim Exceptional Sets for Sums of Cubes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-448
-
- Article
-
- You have access
- Export citation