Contents
Research Article
Existence of solutions of Oseen type integral equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-66
-
- Article
-
- You have access
- Export citation
Comparaison resultats pour la stabilité pratique
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-248
-
- Article
-
- You have access
- Export citation
Small subharmonic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-82
-
- Article
-
- You have access
- Export citation
Monadic representability of certain binary relations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-376
-
- Article
-
- You have access
- Export citation
Analytic mappings with negative coefficients in the unit disc
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-91
-
- Article
-
- You have access
- Export citation
Oscillations in linear systems of differential-difference equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-387
-
- Article
-
- You have access
- Export citation
Perfect McLain groups are superperfect
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-257
-
- Article
-
- You have access
- Export citation
Locally uniformly rotund renorming and decompositions of Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-265
-
- Article
-
- You have access
- Export citation
Stability of functional differential equations of Volterra type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 93-100
-
- Article
-
- You have access
- Export citation
Graphs with Eulerian chains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-399
-
- Article
-
- You have access
- Export citation
The finite difference versus the finite element method for the solution of boundary value problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-288
-
- Article
-
- You have access
- Export citation
Conference in Honour of Kurt Mahler
Some suggestions for further research
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-108
-
- Article
-
- You have access
- Export citation
Research Article
Free products of locally indicable groups with a single relator
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-404
-
- Article
-
- You have access
- Export citation
Decompositions of graphs of modules over semisimple rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-413
-
- Article
-
- You have access
- Export citation
Conference in Honour of Kurt Mahler
p-adic methods in the study of Taylor coefficients of rational functions*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-117
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 29 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Conference in Honour of Kurt Mahler
The n-dimensional approximation constatant*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 119-125
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 29 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Epimorphisms and semigroup varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-417
-
- Article
-
- You have access
- Export citation
Conference in Honour of Kurt Mahler
A method of Mahler in transcendence theory and some of its applications*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
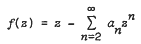 be analytic in the unit disc
be analytic in the unit disc 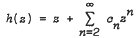 with
with 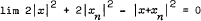 . It is shown that such an equivalent norm exists on every Banach space
. It is shown that such an equivalent norm exists on every Banach space