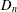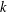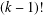Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Staš, Michal
2019.
Determining Crossing Number of Join of the Discrete Graph with Two Symmetric Graphs of Order Five.
Symmetry,
Vol. 11,
Issue. 2,
p.
123.
STAŠ, MICHAL
2020.
ON THE CROSSING NUMBER OF THE JOIN OF THE WHEEL ON FIVE VERTICES WITH THE DISCRETE GRAPH.
Bulletin of the Australian Mathematical Society,
Vol. 101,
Issue. 3,
p.
353.
BEREZNY, STEFAN
and
STAS, MICHAL
2020.
On the crossing number of join of the wheel on six vertices with the discrete graph.
Carpathian Journal of Mathematics,
Vol. 36,
Issue. 3,
p.
381.
Staš, Michal
2020.
On the Crossing Numbers of the Joining of a Specific Graph on Six Vertices with the Discrete Graph.
Symmetry,
Vol. 12,
Issue. 1,
p.
135.
Staš, Michal
2021.
On the Crossing Numbers of the Join Products of Six Graphs of Order Six with Paths and Cycles.
Symmetry,
Vol. 13,
Issue. 12,
p.
2441.
Fortes, Jana
and
Staš, Michal
2023.
Crossing Numbers of Join Product with Discrete Graphs: A Study on 6-Vertex Graphs.
Mathematics,
Vol. 11,
Issue. 13,
p.
2960.