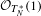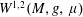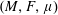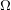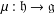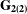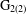Refine listing
Actions for selected content:
476 results in 53Cxx
Metrizability of Holonomy Invariant Projective Deformation of Sprays
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 January 2020, pp. 701-714
- Print publication:
- September 2023
-
- Article
- Export citation
EXISTENCE AND COMPACTNESS THEORY FOR ALE SCALAR-FLAT KÄHLER SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 10 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
Nearly Parallel G2-structures with Large Symmetry Group
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 December 2019, pp. 339-359
- Print publication:
- April 2021
-
- Article
- Export citation
Open problems and questions about geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 641-684
- Print publication:
- March 2021
-
- Article
- Export citation
Simplicial complexity of surface groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 3153-3162
- Print publication:
- December 2020
-
- Article
- Export citation
PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1371-1408
- Print publication:
- July 2021
-
- Article
- Export citation
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1023-1038
- Print publication:
- May 2021
-
- Article
- Export citation
Dispersionless integrable hierarchies and GL(2, ℝ) geometry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 129-154
- Print publication:
- January 2021
-
- Article
- Export citation
Infinitesimal Hilbertianity of Weighted Riemannian Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 118-140
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Zariski closures of images of algebraic subsets under the uniformization map on finite-volume quotients of the complex unit ball
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 19 September 2019, pp. 2129-2149
- Print publication:
- November 2019
-
- Article
- Export citation
ON ALMOST STABLE CMC HYPERSURFACES IN MANIFOLDS OF BOUNDED SECTIONAL CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 September 2019, pp. 333-338
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Locality in the Fukaya category of a hyperkähler manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1924-1958
- Print publication:
- October 2019
-
- Article
- Export citation
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
ON COMPACT HOMOGENEOUS
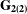 $\mathbf{\text{G}_{2(2)}}$-MANIFOLDS
$\mathbf{\text{G}_{2(2)}}$-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 71-80
- Print publication:
- February 2021
-
- Article
- Export citation
Isospectrality for Orbifold Lens Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 281-325
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
Open manifolds with non-homeomorphic positively curved souls
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 357-376
- Print publication:
- September 2020
-
- Article
- Export citation
Topological rigidity for closed hypersurfaces of elliptic space forms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 20 June 2019, pp. 1063-1072
-
- Article
- Export citation
Real Hypersurfaces in the Complex Quadric with Lie Invariant Structure Jacobi Operator
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 10 June 2019, pp. 204-221
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
The Classification of 7- and 8-dimensional Naturally Reductive Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 30 May 2019, pp. 1246-1274
- Print publication:
- October 2020
-
- Article
- Export citation