Refine search
Actions for selected content:
12 results
REIDEMEISTER’S THEOREM USING TRANSVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 356-367
- Print publication:
- April 2025
-
- Article
- Export citation
TRANSVERSALITY, REGULARITY AND ERROR BOUNDS IN VARIATIONAL ANALYSIS AND OPTIMISATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 167-169
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Non-dense orbits on homogeneous spaces and applications to geometry and number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1327-1372
- Print publication:
- April 2022
-
- Article
- Export citation
Sharp Bertini Theorem for Plane Curves over Finite Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 223-230
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
METRIC REGULARITY—A SURVEY PART II. APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 376-417
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Law and Social Theory: Three Problems
-
- Journal:
- Asian Journal of Law and Society / Volume 1 / Issue 2 / November 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 235-254
-
- Article
-
- You have access
- HTML
- Export citation
How humans fly
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1030-1054
- Print publication:
- October 2013
-
- Article
- Export citation
Transversality theorem in o-minimal structures
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1227-1234
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
CONSTANT HIGHER-ORDER MEAN CURVATURE HYPERSURFACES IN RIEMANNIAN SPACES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 5 / Issue 4 / October 2006
- Published online by Cambridge University Press:
- 09 June 2006, pp. 527-562
- Print publication:
- October 2006
-
- Article
- Export citation
The Stability Theorems for Subgroups of
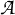 and
and 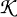
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 5 / 01 October 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 995-1006
- Print publication:
- 01 October 1994
-
- Article
-
- You have access
- Export citation

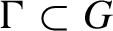
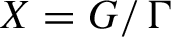
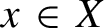
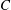
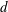
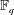
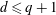
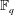
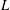
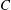
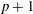
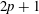
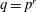
 and
and