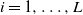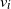Refine search
Actions for selected content:
1 results
Optimal redundancy allocation in coherent systems with heterogeneous dependent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2022, pp. 1144-1177
- Print publication:
- December 2022
-
- Article
- Export citation