Article contents
Optimal redundancy allocation in coherent systems with heterogeneous dependent components
Published online by Cambridge University Press: 25 August 2022
Abstract
This paper is concerned with the optimal number of redundant allocation to n-component coherent systems consisting of heterogeneous dependent components. We assume that the system is built up of L groups of different components, 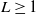 $L\geq 1$, where there are
$L\geq 1$, where there are 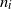 $n_i$ components in group i, and
$n_i$ components in group i, and 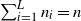 $\sum_{i=1}^{L}n_i=n$. The problem of interest is to allocate
$\sum_{i=1}^{L}n_i=n$. The problem of interest is to allocate 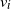 $v_i$ active redundant components to each component of type i,
$v_i$ active redundant components to each component of type i, 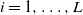 $i=1,\dots, L$. To get the optimal values of
$i=1,\dots, L$. To get the optimal values of 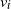 $v_i$ we propose two cost-based criteria. One of them is introduced based on the costs of renewing the failed components and the costs of refreshing the alive ones at the system failure time. The other criterion is proposed based on the costs of replacing the system at its failure time or at a predetermined time
$v_i$ we propose two cost-based criteria. One of them is introduced based on the costs of renewing the failed components and the costs of refreshing the alive ones at the system failure time. The other criterion is proposed based on the costs of replacing the system at its failure time or at a predetermined time  $\tau$, whichever occurs first. The expressions for the proposed functions are derived using the mixture representation of the system reliability function based on the notion of survival signature. We assume that a given copula function models the dependency structure between the components. In the particular case that the system is a series-parallel structure, we provide the formulas for the proposed cost-based functions. The results are discussed numerically for some specific coherent systems.
$\tau$, whichever occurs first. The expressions for the proposed functions are derived using the mixture representation of the system reliability function based on the notion of survival signature. We assume that a given copula function models the dependency structure between the components. In the particular case that the system is a series-parallel structure, we provide the formulas for the proposed cost-based functions. The results are discussed numerically for some specific coherent systems.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 3
- Cited by


