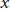Refine search
Actions for selected content:
6 results
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A New Proof of the Hansen—Mullen Irreducibility Conjecture
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1373-1389
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
A Lift of the Schur and Hall–Littlewood Bases to Non-commutative Symmetric Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 3 / 01 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-565
- Print publication:
- 01 June 2014
-
- Article
-
- You have access
- Export citation
On Tensor Products of Polynomial Representations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 4 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 584-592
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
Combinatorial Hopf algebras and generalized Dehn–Sommerville relations
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 13 January 2006, pp. 1-30
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation
Hyperbolic Polynomials and Convex Analysis
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 3 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-488
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation
 .
.