Article contents
A New Proof of the Hansen—Mullen Irreducibility Conjecture
Published online by Cambridge University Press: 20 November 2018
Abstract
We give a new proof of the Hansen–Mullen irreducibility conjecture. The proof relies on an application of a (seemingly new) sufficient condition for the existence of elements of degree  $n$ in the support of functions on finite fields. This connection to irreducible polynomials is made via the least period of the discrete Fourier transform
$n$ in the support of functions on finite fields. This connection to irreducible polynomials is made via the least period of the discrete Fourier transform 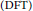 $\left( \text{DFT} \right)$ of functions with values in finite fields. We exploit this relation and prove, in an elementary fashion, that a relevant function related to the
$\left( \text{DFT} \right)$ of functions with values in finite fields. We exploit this relation and prove, in an elementary fashion, that a relevant function related to the 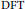 $\text{DFT}$ of characteristic elementary symmetric functions (that produce the coefficients of characteristic polynomials) satisfies a simple requirement on the least period. This bears a sharp contrast to previous techniques employed in the literature to tackle the existence of irreducible polynomials with prescribed coefficients.
$\text{DFT}$ of characteristic elementary symmetric functions (that produce the coefficients of characteristic polynomials) satisfies a simple requirement on the least period. This bears a sharp contrast to previous techniques employed in the literature to tackle the existence of irreducible polynomials with prescribed coefficients.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
- 1
- Cited by

