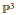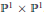Refine search
Actions for selected content:
5 results
Powers of Principal Q-Borel ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 633-652
- Print publication:
- September 2022
-
- Article
- Export citation
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 07 May 2020, pp. 1969-1981
- Print publication:
- November 2021
-
- Article
- Export citation
The Minimal Free Resolution of Fat Almost Complete Intersections in ℙ1 × ℙ1
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 6 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1274-1291
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
Symbolic Powers of Monomial Ideals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 39-55
-
- Article
- Export citation
Symbolic Powers Versus Regular Powers of Ideals of General Points in ℙ1 × ℙ1
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 823-842
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation

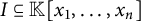
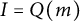
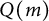



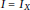
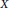
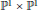
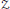
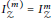
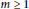
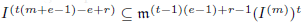 for all positive integers
for all positive integers 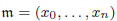 . This captures two conjectures (
. This captures two conjectures (