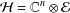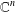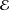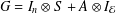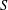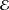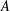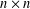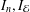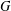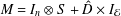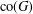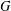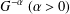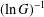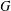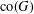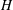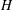Refine search
Actions for selected content:
2 results
SIMILARITY OF OPERATORS ON TENSOR PRODUCTS OF SPACES AND MATRIX DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 19-30
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A BOUND FOR SIMILARITY CONDITION NUMBERS OF UNBOUNDED OPERATORS WITH HILBERT–SCHMIDT HERMITIAN COMPONENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 12 September 2014, pp. 331-342
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation