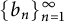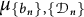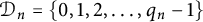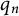Refine search
Actions for selected content:
30 results
How big is a tiling’s return module?
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 2514-2532
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 593-610
- Print publication:
- September 2024
-
- Article
- Export citation
15 - Light Effects across Species in Nature
-
-
- Book:
- Biological Implications of Circadian Disruption
- Published online:
- 07 October 2023
- Print publication:
- 12 October 2023, pp 338-355
-
- Chapter
- Export citation
Unsupervised classification: a necessary step for Deep Learning?
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 19 / Issue S368 / August 2023
- Published online by Cambridge University Press:
- 01 August 2025, pp. 63-66
- Print publication:
- August 2023
-
- Article
- Export citation
4 - The Frequency Domain and Pitch
-
- Book:
- Physics Behind Music
- Published online:
- 24 May 2023
- Print publication:
- 06 April 2023, pp 45-66
-
- Chapter
- Export citation
Appendix I - Nuclear Magnetic Resonance
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 592-595
-
- Chapter
- Export citation
3 - Chromatic Fracture Cubes
-
- Book:
- Equivariant Topology and Derived Algebra
- Published online:
- 29 October 2021
- Print publication:
- 18 November 2021, pp 100-118
-
- Chapter
- Export citation
4 - An Introduction to Algebraic Models for Rational G–Spectra
-
- Book:
- Equivariant Topology and Derived Algebra
- Published online:
- 29 October 2021
- Print publication:
- 18 November 2021, pp 119-179
-
- Chapter
- Export citation
Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2009-2027
- Print publication:
- June 2022
-
- Article
- Export citation
6 - Internal Waves and the Vortical Mode
-
- Book:
- Ocean Mixing
- Published online:
- 10 March 2021
- Print publication:
- 04 February 2021, pp 197-229
-
- Chapter
- Export citation
Introduction
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 1-6
-
- Chapter
- Export citation
4 - Triangulated Categories
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 128-165
-
- Chapter
- Export citation
1 - Basics of Stable Homotopy Theory
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 7-36
-
- Chapter
- Export citation

Foundations of Stable Homotopy Theory
-
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020
Discovery of new changing look in NGC 1566
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 15 / Issue S356 / October 2019
- Published online by Cambridge University Press:
- 29 January 2021, pp. 127-131
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Laboratory studies of Vacuum Ultra-Violet (VUV) emission spectra of heavy element ions
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 15 / Issue S357 / October 2019
- Published online by Cambridge University Press:
- 09 October 2020, pp. 84-88
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
SPECTRA OF LINEAR FRACTIONAL COMPOSITION OPERATORS ON THE GROWTH SPACE AND BLOCH SPACE OF THE UPPER HALF-PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 199-214
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Multitemperature analysis of solar flare observed on 2003 March 29
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 11 / Issue S320 / August 2015
- Published online by Cambridge University Press:
- 09 September 2016, pp. 86-88
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
GalevNB: from simulations to observations
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 12 / Issue S316 / August 2015
- Published online by Cambridge University Press:
- 31 March 2017, pp. 259-260
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
GalevNB: GALEV for N-body simulations
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 10 / Issue S312 / August 2014
- Published online by Cambridge University Press:
- 07 March 2016, pp. 258-259
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation