1 Introduction and results
A basic objective in tiling theory is understanding which properties of a tiling are topological (depending only on the tiling space up to homeomorphism), which are combinatorial (depending on which tiles touch which other tiles), and which are geometric (depending on the shapes and sizes of the individual tiles). In this paper, we relate a geometric object, namely the rank of the return module for large patches P, to a topological object, namely the rank of the first Čech cohomology of the associated tiling space.
Let T be a tiling satisfying some basic axioms (see §2) and let P be a patch. That is, P is a finite set of tiles in T whose relative positions are fixed. The patch P will appear in many different places in T. The position of one occurrence of P relative to another is called a return vector of P. The additive group generated by the return vectors of P is called the return module of P and is denoted
$\mathrm {Ret}(P)$
. The rank of
$\mathrm {Ret}(P)$
is the maximal number of return vectors that are linearly independent over the integers. Equivalently, it is the dimension of
$\mathrm {Ret}(P) \otimes \mathbb {Q}$
as a vector space over the rational numbers
$\mathbb {Q}$
.
If
$P'$
is a patch that contains P, then every return vector of
$P'$
is also a return vector of P, so the rank of
$\mathrm {Ret}(P')$
is at most equal to the rank of P. For any given tiling, there is a limiting rank that applies to the return modules of all sufficiently large patches.
If T is any tiling, then the tiling space
$\Omega _T$
associated with T, also called the continuous hull of T, is the closure of the orbit of T under translations in the ‘big ball’ metric where two tilings are considered close if they agree on a big ball around the origin up to a small translation. There are many cohomology theories associated with T and
$\Omega _T$
. For our purposes, the most useful is the pattern equivariant cohomology [Reference Kellendonk10, Reference Kellendonk and Putnam11] of T, which is isomorphic to the Čech cohomology
$\check H^*(\Omega _T)$
. The rank of
$\check H^1(\Omega _T)$
is the dimension of
$\check H^1(\Omega _T, \mathbb {Q}) = \check H^1(\Omega ) \otimes \mathbb {Q}$
as a vector space over
$\mathbb {Q}$
.
The first of our two main theorems bounds the limiting rank of the return modules by the rank of the cohomology.
Theorem 1.1. Let T be an aperiodic tiling that is repetitive and has finite local complexity. Then, the limiting rank of the return modules of T is bounded by
$\mathrm {Rank} (\check H^1(\Omega _T))$
, the rank of the first Čech cohomology of
$\Omega _T$
.
Note that this theorem only bounds the rank of
$\mathrm {Ret}(P)$
for a sufficiently large patch P. This is what matters, as the return module for large patches determines many of the dynamical properties of a tiling, such as its diffraction spectrum. The return module for small patches does not have any dynamical significance and can often be changed by adding local markings to a tiling. See §5 for examples of this phenomenon.
Before stating our second main theorem, we must introduce the concept of shape changes for tilings. It may happen that two tilings T and
$T'$
have identical combinatorics, with each tile in T having a corresponding tile in
$T'$
, and with two tiles in T touching if and only if the corresponding tiles in
$T'$
touch. However, the shapes and sizes of the tiles in
$T'$
may be different from those in T. In that case, we say that
$T'$
is obtained by applying a shape change to T.
For instance, suppose that T is a Thue–Morse tiling of the line by two kinds of tiles, called a and b, following the sequence
$\ldots abbabaabbaababba \ldots .$
Suppose furthermore that the a and b tiles both have length 1. Now let
$T'$
be a tiling by tiles A and B following the analogous pattern
$\ldots ABBABAABBAABABBA \ldots ,$
only with an A tile having length
$\pi /4$
and a B tile having length
$\sqrt {2}$
. The tilings T and
$T'$
have identical combinatorics but different geometry. Consequently, the spaces
$\Omega _T$
and
$\Omega _{T'}$
are homeomorphic but differ as dynamical systems. The return modules of a patch
$P \subset T$
and a corresponding patch
$P' \subset T'$
do not necessarily have the same rank.
The shape changes to a tiling T of
$\mathbb {R}^d$
, modulo a form of equivalence called mutual local derivability (MLD), are parameterized by an open subset of
$\check H^1(\Omega _T) \otimes \mathbb {R}^d$
[Reference Clark and Sadun6]. We say that a property of tilings in this family is generic if it occurs for all shapes except for a set of measure zero. (The concept of measure zero is clear when
$\check H^1$
has finite rank, as we are then dealing with a Euclidean space. If
$\check H^1$
has infinite rank, then the set of possible shape changes is a union of finite dimensional spaces. In that case, we say that a property is generic if it applies on a set of full measure on each of these spaces.)
Our second main theorem says that generic shape changes result in the largest possible return modules.
Theorem 1.2. Let T be an aperiodic tiling that is repetitive and has finite local complexity and suppose that
$\ell = \mathrm {Rank}(\check H^1(\Omega _T))$
. Then, after applying a generic shape change, the rank of every return module is at least
$\ell $
.
Combining the two theorems, we obtain the following corollary.
Corollary 1.3. Let T be an aperiodic tiling that is repetitive and has finite local complexity and suppose that
$\ell = \mathrm {Rank}(\check H^1(\Omega _T))$
. Then, after applying a generic shape change, the limiting rank of the return modules of T is exactly
$\ell $
.
For simplicity, we have written Theorem 1.2 and Corollary 1.3 assuming that
$\check H^1(\Omega _T)$
has finite rank. When
$\check H^1$
has infinite rank, we can restrict our attention to a rank-
$\ell $
subgroup
$H^1_{\ell } \subset \check H^1$
. Our proof of Theorem 1.2 actually shows that, for a generic shape change with parameters in
$H^1_\ell \otimes \mathbb {R}^d$
, the rank of the return module of every patch will be at least
$\ell $
. Since we can choose
$\ell $
to be as large as we wish, there is no upper bound to the limiting ranks of return modules.
The dynamical spectrum of a tiling space is closely associated with return modules of large patches. Suppose that a large patch P occurs at two locations x and y. Then,
$T-x$
and
$T-y$
agree on a large ball around the origin and so are close in the tiling metric (see §2 for precise definitions). If f is a continuous function on
$\Omega _T$
, then
$f(T-y) \approx f(T-y)$
. In particular, if f is a continuous eigenfunction of translation with eigenvalue
$\unicode{x3bb} $
, then
$$ \begin{align*} \exp(2 \pi i \unicode{x3bb} \cdot (x-y)) \approx 1, \end{align*} $$
with the approximation getting increasingly better as P gets bigger and bigger. In most tilings of interest (in particular, in all primitive substitution tilings), all measurable eigenfunctions can be chosen continuous, so this constraint applies to all eigenvalues of translation.
Solomyak [Reference Solomyak19] used this observation to relate the point spectrum of a substitution tiling to the set of return vectors and to the stretching factor. Baake and Moody [Reference Baake and Moody5] went further, using the return module of a tiling with pure point spectrum to reconstruct its cut-and-project structure. For a recent generalization of the Baake–Moody construction, see [Reference Strungaru, Baake and Grimm20].
2 Definitions and notation
In this section, we review the basics of tilings, tiling spaces, and return modules. For a more comprehensive review, see [Reference Baake and Grimm4, Reference Sadun14].
A tile is a (closed) topological ball that is the closure of its interior. In addition to its geometry, a tile may carry a label to distinguish it from other tiles of the same size and shape. If two tiles carry the same label, then each must be a translate of the other. A tiling of
$\mathbb {R}^d$
is a collection of tiles whose union is all of
$\mathbb {R}^d$
and whose interiors are disjoint. A patch of a tiling is a finite subset of its tiles. A tiling is said to have finite local complexity, or FLC, if for each
$r>0$
, there are only finitely many patches, up to translation, of diameter up to r. Equivalently, a tiling has FLC if two conditions are met:
-
(1) there are only finitely many tile types, up to translation; and
-
(2) there are only finitely many connected 2-tile patches, up to translation. That is, there are only finitely many ways for one tile to touch another.
The group
$\mathbb {R}^d$
of translations acts on tiles by shifting their positions but leaving their labels unchanged. By extension,
$\mathbb {R}^d$
acts on tilings and on patches by translating all of the tiles simultaneously. The action of
$x \in \mathbb {R}^d$
on a tiling T is denoted
$T+x$
. A tiling T is said to be aperiodic if
$T+x = T$
implies
$x=0$
. The orbit of a tiling T under translation is denoted
$\mathcal {O}(T)$
.
We will frequently consider a particular pattern of adjacent tiles, such as the pattern
$P=aaba$
in a Thue–Morse tiling, without specifying the location of P. Strictly speaking, P is an equivalence class of patches under translation rather than a specific patch, but we will abuse notation and terminology by calling P a ‘patch’ anyway. We can then talk about multiple occurrences of P in a tiling, that is, multiple patches in the equivalence class defined by P.
On the set of all tilings by a given set of tile types, we consider the topology induced by the big ball metric, in which two tilings T and
$T'$
are considered
$\epsilon $
-close if they agree on a ball of radius
$1/\epsilon $
around the origin, up to translation of each by a distance
$\epsilon /2$
or less. A tiling space is a non-empty translation-invariant set of tilings that is closed in this topology.
We can obtain a tiling space from any tiling T by taking the closure of
$\mathcal {O}(T)$
. This space is called the continuous hull of T and is denoted
$\Omega _T$
. It is the smallest tiling space that contains T. A tiling
$T'$
is in
$\Omega _T$
if and only if every patch of
$T'$
is a translate of a patch in T.
A tiling T is said to be repetitive if for every patch
$P \subset T$
, there exists a radius
$r(P)$
, called the repetitivity radius of P, such that every ball of radius
$r(P)$
contains at least one copy of P. This is equivalent to
$\Omega _T$
being a minimal dynamical system. That is, every orbit is dense, so for each
$T' \in \Omega _T$
,
$\Omega _{T'} = \Omega _T$
. In that case, any two tilings
$T_1,T_2 \in \Omega _T$
have exactly the same patches (up to translation), so any quantity based on those patches is the same for both tilings.
Suppose that T and
$T'$
are two tilings with the following property: there is a radius r such that, for all
$x, y \in \mathbb {R}^d$
such that
$T-x$
and
$T-y$
agree on a ball of radius r around the origin,
$T'-x$
and
$T'-y$
agree on a ball of radius 1 around the origin. This is a precise way of saying that the patterns of
$T'$
are determined in a local way from the patterns of T in the exact same locations. If this condition is met, then we say that
$T'$
is locally derivable, or LD, from T. If
$T'$
is LD from T and T is LD from
$T'$
, then T and
$T'$
are mutually locally derivable, or MLD. The local rule deriving T from
$T'$
extends to a topological conjugacy from
$\Omega _T$
to
$\Omega _{T'}$
that we call an MLD equivalence.
In principle, the tiles in a tiling may have very complicated (say, fractal) boundaries. However, every FLC tiling is MLD to a tiling whose tiles are convex polygons (or polytopes) that meet full edge to full edge. We can therefore assume, with no loss of generality, that our tilings are of this sort.
The procedure for doing this conversion is called the ‘Voronoi trick’. It involves first picking a ‘control point’ for each tile (or for each instance of a more complicated patch P) and replacing the tiling with a point pattern, and then replacing each point in the point pattern with its ‘Voronoi cell’ consisting of all points in
$\mathbb {R}^d$
that are closer to the given control point than to any other control point. For more information on the Voronoi trick, see [Reference Baake and Grimm4] or [Reference Sadun14].
Now pick a patch P and pick a control point within P to represent the patch. (For instance, we might pick the control point of the pattern
$abaa$
to be the left endpoint of the b tile.) When we speak of the locations of P in a tiling, we mean the locations of the control point. Let
$\{x_1, x_2, \ldots \}$
be all the locations of P in T. The relative positions
$x_i-x_j$
are called return vectors for P and do not depend on the choice of control point. The span (over
$\hspace {0.5pt}\mathbb {Z}$
) of the return vectors is called the return module of P and is denoted
$\mathrm {Ret}(P)$
. The fact that
$x_i-x_j$
is a return vector is a property of the ball of radius slightly larger than
$|x_i-x_j|/2$
centered at the point
$(x_i+x_j)/2$
. If T is repetitive, then a copy of this large ball appears in every
$T' \in \Omega _T$
, so
$x_i-x_j$
is also a return vector for P in
$T'$
. The set of return vectors and the resulting return module are thus quantities that we can associate with the tiling space
$\Omega _T$
rather than with just the specific tiling T.
If P and
$P'$
are patches with
$P \subset P'$
, then every return vector of
$P'$
is also a return vector of P, so
$\mathrm {Ret}(P') \subset \mathrm {Ret}(P)$
and
$\mathrm {Rank}(\mathrm {Ret}(P')) \le \mathrm {Rank}(\mathrm {Ret}(P))$
. We are interested in the limit of this rank as the patches grow in size. More precisely, there is a minimum k among the ranks of all return modules and there exists a patch
$\hat P$
whose return module achieves that minimal rank. Any patch that contains
$\hat P$
must also have a return module of rank k. If T is repetitive, then every sufficiently large patch (specifically, any patch of size bigger than the repetitivity radius of
$\hat P$
) contains a copy of
$\hat P$
and so has a return module of rank k. We call k the limiting rank of the return modules of T.
Note that we are taking the limit of the rank, not the rank of the limit! In some tilings, the return module for a large patch can be smaller than, but of the same rank as, the return module for a small patch. For instance, in the Thue–Morse tiling with a and b tiles both having length 1, the return module for the one-letter patch
$P_1=a$
is
$\hspace {0.5pt}\mathbb {Z}$
, while the return module of
$P_1=abb$
is
$2\hspace {0.5pt}\mathbb {Z}$
; there are other patches whose return modules are
$4\hspace {0.5pt}\mathbb {Z}$
,
$8\hspace {0.5pt}\mathbb {Z}$
, etc. The limit of these modules is the rank-0 set
$\{0\}$
. However, the rank of
$2^n \hspace {0.5pt}\mathbb {Z}$
is 1 for all n, so the limiting rank is 1. (In other tilings, such as the Fibonacci tiling, all patches have the same return module and there is no need to take a limit at all.)
If two tilings T and
$T'$
are MLD equivalent, then the limiting ranks of their return modules must be equal. If P is a patch in T, then there is a (typically larger) patch
$P'$
in
$T'$
such that every appearance of
$P'$
in
$T'$
is associated with the appearance of a P in T. The return module of
$P'$
is then a subset of the return module of P. Thus, the minimal rank of a return module in
$T'$
is no greater than the minimal rank of a return module in T. Repeating the argument with the roles of T and
$T'$
reversed, we see that the (minimal and) limiting ranks for the two tilings are the same.
However, MLD invariance does not imply that limiting rank is preserved by all topological conjugacies of tiling spaces. We will see in the examples that there are topologically conjugate versions of the Fibonacci tiling with different limiting ranks.
3 Tiling cohomology
The precise definition of the Čech cohomology of a space is complicated, involving open covers, nerves of said covers, the simplicial cohomology of those nerves, and a limit over all open covers partially ordered by refinement [Reference Hatcher8]. Fortunately, those details are not needed for a working understanding of tiling cohomology. For our purposes, two facts are sufficient [Reference Sadun, Kellendonk, Lenz and Savinien15]:
-
(1) the Čech cohomology of a CW complex is isomorphic to the singular cohomology, which in turn is isomorphic to many other cohomology theories. On a CW complex, ‘all cohomologies are the same’;
-
(2) the Čech cohomology of an inverse limit space is the direct limit of the Čech cohomologies of the approximants.
Tiling spaces are not CW complexes, but they are inverse limits of CW complexes. Each approximant, called an Anderson–Putnam complex, describes the tiling in a neighborhood of the origin. A point in the inverse limit of the approximants is a set of consistent instructions for tiling increasingly bigger portions of
$\mathbb {R}^d$
. The union of the neighborhoods is all of
$\mathbb {R}^d$
, so a point in the inverse limit is a set of instructions for tiling all of space, which is tantamount to a tiling itself. There are numerous ways to construct approximants for tiling spaces, but they are all qualitatively similar. The key ideas are due to Anderson and Putnam [Reference Anderson and Putnam1] and to Gähler [Reference Gähler7]. See [Reference Sadun12] for a unification of their arguments and [Reference Sadun14] for a review.
The upshot is that the Čech cohomology of a tiling space is constructed from data about the local structure of a tiling, where ‘local’ can include information out to any finite distance but not out to infinity. This idea was codified by Kellendonk and Putnam [Reference Kellendonk10, Reference Kellendonk and Putnam11] as a new cohomology theory called pattern equivariant (PE) cohomology.
Consider a reference tiling T of
$\mathbb {R}^d$
and a function
$f: \mathbb {R}^d \to \mathbb {R}$
. We say that a function
$f: \mathbb {R}^d \to \mathbb {R}$
is PE with radius r if its value at a point x depends only on the form of T in a ball of radius r around x. More precisely, if f is PE with radius r and if
$T-x_1$
and
$T-x_2$
agree on a ball of radius r around the origin, then
$f(x_1)=f(x_2)$
. A function is said to be PE (without any qualifiers) if it is PE with some finite radius. We can likewise define PE differential forms. It is easy to check that the exterior derivative of a PE form is PE. Kellendonk and Putnam defined the (real-valued) PE cohomology of a tiling T to be
$$ \begin{align*} H^k_{PE}(T) = \frac{\text{Closed PE } k\text{-forms}}{d(\text{PE } k-1\text{-forms})} \end{align*} $$
and proved that
$H^k_{PE}(T)$
was isomorphic to
$\check H^k(\Omega _T) \otimes \mathbb {R}$
.
To obtain an integer version of PE cohomology, we can consider PE cochains. A PE k-cochain with radius r assigns an integer to every k-cell in the tiling T based on the neighborhood of size r around that k-cell. (If T does not have clearly defined vertices, edges, faces, etc., apply the Voronoi trick to convert T into a tiling that does.) That is, if the tiling is the same within some fixed distance r of two different k-cells, then our function must assign the same value to both cells. A cochain is said to be PE if it is PE with some radius.
The coboundary of a cochain is defined the same as with ordinary (not PE) cochains. If
$\alpha $
is a k-cochain and c is a
$(k+1)$
-cell, then
$\delta \alpha $
is a
$(k+1)$
-cochain whose value on c is
$$ \begin{align*} \delta \alpha (c) := \alpha(\partial c), \end{align*} $$
where
$\partial c$
is the boundary of c. The coboundary of a PE cochain is PE (although possibly with a slightly larger radius). Sadun [Reference Sadun13] defined the integer-valued PE cohomology of T to be
$$ \begin{align*} H^k_{PE}(T) = \frac{\text{Closed PE } k\text{-cochains}}{\delta(\text{PE } (k-1)\text{-cochains})} \end{align*} $$
and proved that this was isomorphic to
$\check H^k(\Omega _T)$
. The same construction works with values in any Abelian group, not just the integers
$\hspace {0.5pt}\mathbb {Z}$
.
We are interested in the rank of
$\check H^1(\Omega _T)$
. This is the same as the dimension over
$\mathbb {Q}$
of
$\check H^1(\Omega _T) \otimes \mathbb {Q}$
, which is naturally isomorphic to
$H^1_{PE}(T,\mathbb {Q})$
, the first PE cohomology of T with values in
$\mathbb {Q}$
. All of our calculations will be done in the PE setting, where we represent cohomology classes with cochains on T.
The following theorem will allow us to restrict our attention to return vectors of large patches.
Theorem 3.1. Let P be a patch in a repetitive tiling T and suppose that the locations of P are
$\{x_1, x_2, \ldots \}$
. If
$\alpha $
is a closed PE 1-cochain, then the cohomology class of
$\alpha $
depends only on the value of
$\alpha $
applied to paths from
$x_i$
to
$x_j$
. That is:
-
(1) if a closed PE 1-cochain
$\alpha $
evaluates to zero on a path from
$x_i$
to
$x_j$
for each pair
$(i,j)$
, then
$\alpha $
represents the zero cohomology class; -
(2) if two closed PE 1-cochains
$\alpha $
and
$\beta $
give the same values on a path from each
$x_i$
to each other
$x_j$
, then
$\alpha $
and
$\beta $
represent the same cohomology class.
Proof. We begin with the first statement. Let
$r_1$
be the PE radius of
$\alpha $
and let
$r_2$
be the repetitivity radius of P. For each vertex z in our tiling, let
$f(z) = \alpha (c)$
, where c is a path from
$x_1$
to z. (Since
$\alpha $
is closed, this does not depend on our choice of path.) We manifestly have
$\alpha = \delta f$
.
We pick our path c to be the concatenation of two paths
$c_1$
and
$c_2$
, where
$c_1$
goes from
$x_1$
to an
$x_i$
that is close to z and
$c_2$
goes from
$x_i$
to z. See Figure 1. We can also pick the path
$c_2$
to stay within a distance
$r_2$
of z. Since
$\alpha (c_1)=0$
,
$f(z)=\alpha (c_2)$
. However,
$\alpha (c_2)$
only depends on the pattern T within a distance
$r_1$
of all of the edges in
$c_2$
, and therefore within a distance
$r_1+r_2$
of z. This makes f a PE function with radius
$r_1+r_2$
. Since
$\alpha $
is the coboundary of a PE function,
$\alpha $
represents the zero class in cohomology.
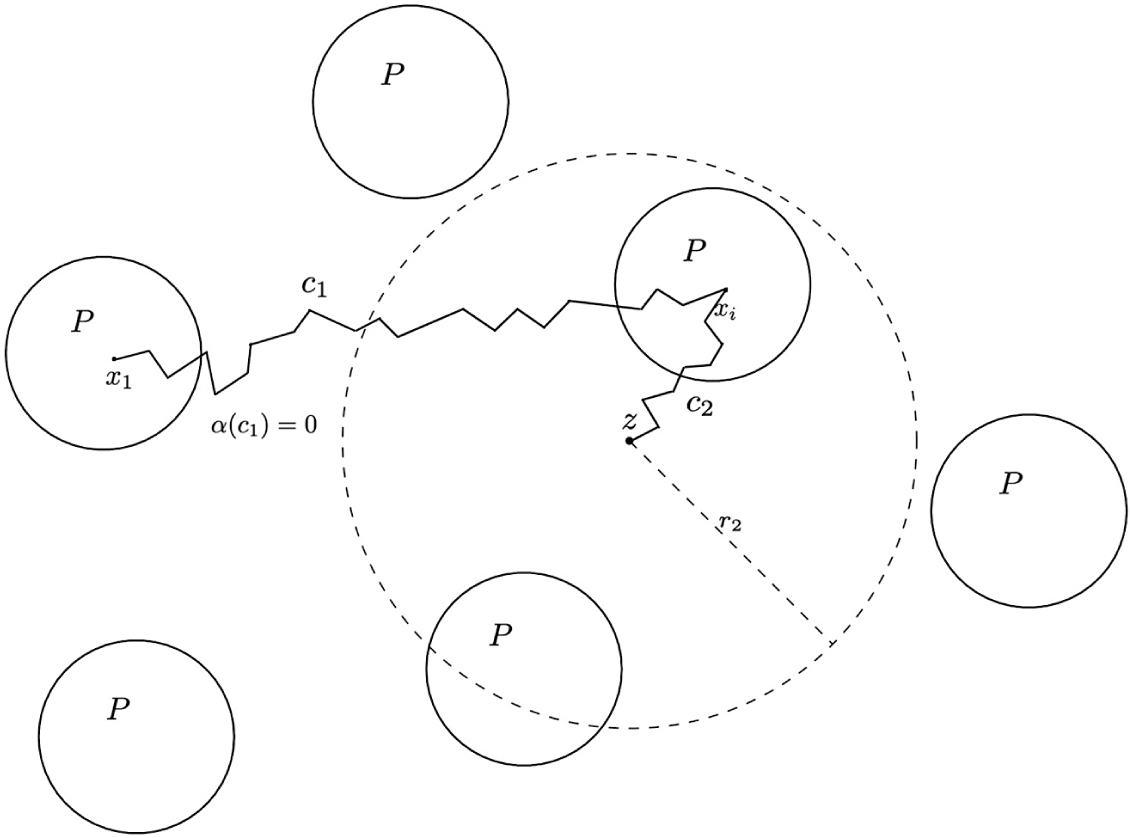
Figure 1 The function
$f(z) = \alpha (c_1)+\alpha (c_2) = \alpha (c_2)$
is pattern-equivariant with radius
$r_1+r_2$
.
For the second statement, we simply apply the first statement to
$\alpha - \beta $
. Since
$\alpha -\beta $
evaluates to zero on all paths from
$x_i$
to
$x_j$
, the class of
$\alpha -\beta $
is zero, so the class of
$\alpha $
is the same as the class of
$\beta $
.
In fact, we can go a step beyond Theorem 3.1. Using a dual version of the Voronoi trick, we can construct a tiling
$T'$
, MLD to the original tiling T, whose vertices are the points
$x_1, x_2, \ldots $
. Since
$\Omega _T$
and
$\Omega _{T'}$
are homeomorphic, we can identify the Čech cohomology of
$\Omega _T$
with the Čech cohomology of
$\Omega _{T'}$
, which in turn is isomorphic to the PE cohomology of
$T'$
. As a result, we can represent classes in
$\check H^1(\Omega _T)$
with closed PE 1-cochains on
$T'$
. That is, we can represent classes in
$\check H^1(\Omega _T)$
as functions on edges in
$T'$
that connect pairs of locations of P in T. In particular, every linear function
$L: \mathrm {Ret}(P) \to \hspace {0.5pt}\mathbb {Z}$
defines a cohomology class in
$\check H^1(\Omega _T)$
that we denote
$\phi (L)$
.
4 Proofs of main theorems
Proof of Theorem 1.1
Let k be the limiting rank of the return modules of T and let P be any patch whose return module has rank k. As noted in the comment after the proof of Theorem 3.1, every linear function
$L: \mathrm {Ret}(P) \to \hspace {0.5pt}\mathbb {Z}$
defines a closed 1-cochain
$\alpha _L$
on an associated tiling
$T'$
whose vertices are the locations of P in T, and thus defines a cohomology class
$\phi (L) \in H^1_{PE}(T') \simeq \check H^1(\Omega _T)$
.
We claim that the map
$\phi $
from linear functions to cohomology classes is injective. To see this, suppose that
$\phi (L)$
is the zero class in cohomology. Then the 1-cochain
$\alpha _L$
on
$T'$
that is defined by L must be a coboundary:
$$ \begin{align*} \alpha_L = \delta f, \end{align*} $$
where f is a PE function with some radius r. Let
$P'$
be a patch of
$T'$
containing a ball of radius r centered at a point
$x_i$
. Then,
$\alpha $
applied to any return vector of
$P'$
must be zero, insofar as f takes on the same value at the endpoints of a chain connecting two instances of
$P'$
. Thus, L restricted to
$\mathrm {Ret}(P') \subset \mathrm {Ret}(P)$
is zero.
However, the rank of
$\mathrm {Ret}(P)$
is already the minimum among all patches of T. This implies that
$\mathrm {Ret}(P')$
is a submodule of
$\mathrm {Ret}(P)$
of full rank, so the only linear function on
$\mathrm {Ret}(P)$
that vanishes on
$\mathrm {Ret}(P')$
is the zero function. That is,
$\phi (L)=0$
implies
$L=0$
, so
$\phi $
is injective.
The rank of
$\mathrm {Ret}(P)$
is the same as the rank of the space of linear functions
$\mathrm {Ret}(P) \to \hspace {0.5pt}\mathbb {Z}$
, which (by the injectivity of
$\phi $
) is the same as the rank of the image of
$\phi $
, which is bounded by the rank of
$\check H^1(\Omega _T)$
. Thus, the limiting rank k is bounded by the rank of
$\check H^1(\Omega _T)$
.
Before proving Theorem 1.2, we review the way that the shapes and sizes of all tiles are parameterized by cochains. In any tiling T, there is a vector-valued cochain
$\mathcal {F}(T)$
, called the fundamental shape cochain of T, that assigns to every edge the actual displacement along that edge. This cochain is closed, since the net displacement along the boundary of any 2-face is zero. The corresponding class
$[\mathcal {F}(T)] \in H^1_{PE}(T,\mathbb {R}^d)$
is called the fundamental shape class.
To obtain a tiling with the same combinatorics as T but different geometry, we deform the cochain
$\mathcal {F}(T)$
into another cochain S. That is, we construct a new tiling (denoted
$S(T)$
) whose vertices, edge, faces, etc. are in 1–1 correspondence with those of T, carrying the same labels, such that the relative position of any pair of vertices in
$S(T)$
is given by S applied to a path connecting the corresponding vertices of T. See Figure 2 for an example.
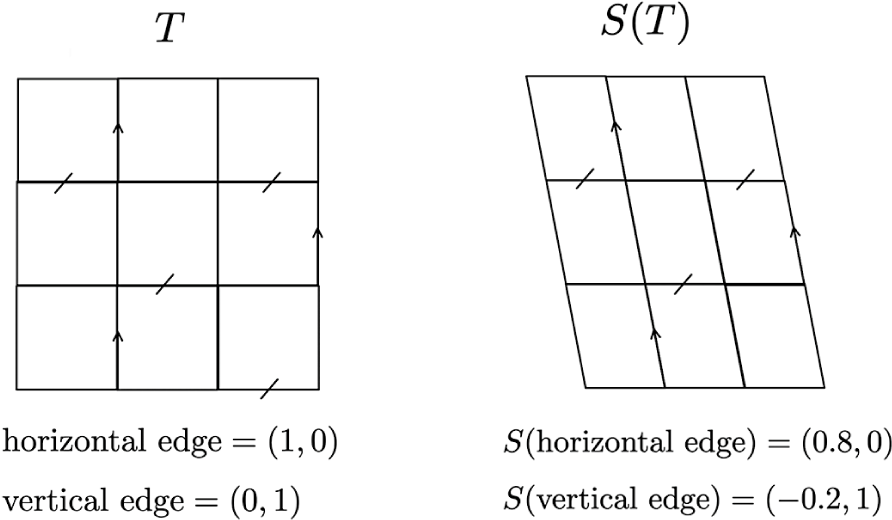
Figure 2 By changing the shape cochain to S, we convert a tiling by squares into a tiling by parallelograms.
For the tiles of
$S(T)$
to fit together and preserve finite local complexity, we need three conditions:
-
• the (vector-valued) cochain S must be PE;
-
• S must be closed; and
-
• the new shapes must not turn any of the tiles inside-out. If
$d=2$
, this is equivalent to the boundary of each tile being a positively oriented simple closed curve. (Figure-eights are not allowed!) In higher dimensions, the condition is similar, although trickier to describe.
The third condition is open. That is, any closed PE cochain S that is close to
$\mathcal {F}(T)$
will automatically satisfy it. As long as we concentrate on small shape changes, we only need to keep track of the first two conditions.
(While not needed for this paper, large shape change classes are indeed possible. Given a cochain S that turns some tiles inside-out, it is usually possible to find another closed PE cochain
$\tilde S$
, cohomologous to S, that satisfies the third requirement. The set of classes in
$H^1_{PE}(T,\mathbb {R}^d)$
that can be realized as fundamental shape classes is dense, open, and of full measure. See [Reference Julien and Sadun9] for details.)
In general, if A is any object associated with T, then we write
$S(A)$
to denote the corresponding object in
$S(T)$
, and if B is any object in
$S(T)$
, then we write
$S^{-1}(B)$
to denote the corresponding object in T. Thus, the hull of
$S(T)$
is
$S(\Omega _T) = \Omega _{S(T)}$
, and for each patch P in T, we are interested in the rank of
$\mathrm {Ret}(S(P))$
.
Note that
$\Omega _T$
and
$S(\Omega _T)$
are homeomorphic and so have identical cohomology groups. All statements about cohomology apply both to T and to
$S(T)$
.
If the rank of
$\check H^1(\Omega _T)$
is
$\ell $
, then
$\check H^1(\Omega _T,\mathbb {R}^d) \simeq \mathbb {R}^{\ell d}$
is an Euclidean space. On this space, the sets of zero (Lebesgue) measure are clearly defined. The essence of Theorem 1.2 is that, after applying a shape change with the class of S avoiding a certain set of measure zero, we obtain return modules of rank at least
$\ell $
.
Proof of Theorem 1.2
Let
$e_1, \ldots , e_d$
be the standard basis for
$\mathbb {R}^d$
. Since
$\mathbb {R}^d$
has infinite dimension over
$\mathbb {Q}$
, we can find
$\ell $
vectors
$w_1, \ldots , w_\ell \in \mathbb {R}^d$
such that
$(e_1,\ldots ,e_d,w_1,\ldots ,w_\ell )$
are linearly independent over
$\mathbb {Q}$
. That is, there is no way to write 0 as a non-trivial linear combination of these vectors with rational coefficients. Among all
$\ell $
-tuples of vectors in
$\mathbb {R}^d$
, those that meet this condition have full measure, since there are only countably many possible rational linear combinations and each one is zero only on a set of codimension d. We can also shrink the vectors
$w_i$
by an integer factor to make them arbitrarily small without affecting linear independence over
$\mathbb {Q}$
.
Since the rank of
$\check H^1(\Omega _T)$
is
$\ell $
, we can choose
$\ell $
closed PE cochains
$\alpha _1, \ldots , \alpha _\ell $
whose classes form a linearly independent set in
$H^1_{PE}(T, \mathbb {Q}) \simeq \check H^1(\Omega _T) \otimes \mathbb {Q}$
.
We do our shape change in two steps. First, we change to a new cochain
$S_0$
that evaluates to a rational vector on each edge. The set of such rational shape cochains is dense in the set of all shape cochains [Reference Sadun and Williams16], so we can pick
$S_0$
arbitrarily close to our original
$\mathcal {F}(T)$
. We then define
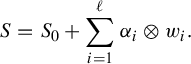$$ \begin{align*} S = S_0 + \sum_{i=1}^\ell \alpha_i \otimes w_i. \end{align*}$$
What remains is picking an arbitrary patch P in T and showing that
$\mathrm {Rank}(\mathrm {Ret}(S(P))) \ge \ell $
.
The displacement along any edge e of
$S(T)$
, which is the same as S applied to
$S^{-1}(e)$
, is a rational vector (namely the contribution of
$S_0$
) plus a rational linear combination of the
$w_i$
vectors. Let
$I_i$
, applied to a rational linear combination of
$(e_1,\ldots ,e_d,w_1,\ldots ,w_\ell )$
, give the coefficient of
$w_i$
. This applies in particular to the return vectors of
$S(P)$
and indeed to all elements of
$\mathrm {Ret}(S(P))$
. Note that if
$v_1$
and
$v_2$
are vertices in T, then
$I_i$
applied to the displacement
$S(v_2)-S(v_1)$
is the same as
$c_i$
applied to a 1-chain from
$v_1$
to
$v_2$
. The collection
$(I_1, \ldots , I_\ell )$
defines a linear map
$\varphi : \mathrm {Ret}(S(P)) \to \mathbb {Q}^\ell $
. We claim that the image of
$\varphi $
has rank
$\ell $
, which then implies that
$\mathrm {Ret}(S(P))$
has rank at least
$\ell $
, as claimed in Theorem 1.2.
To see that the image of
$\varphi $
contains
$\ell $
linearly independent elements, suppose otherwise. Then, there exists a non-zero vector
$b= (b_1,\ldots ,b_\ell ) \in \mathbb {Q}^\ell $
that is orthogonal to
$\varphi (v)$
for every return vector v of
$S(P)$
. However,
$$ \begin{align*} 0 = b \cdot v = \sum (b_i \alpha_i) (S^{-1}(v)). \end{align*} $$
This implies that
$\sum b_i \alpha _i$
evaluates to zero on all return vectors of P. By Theorem 3.1, this then implies that the cohomology class of
$\sum b_i \alpha _i$
is zero. However, the cochains
$\alpha _i$
were assumed to represent linearly independent cohomology classes and b was assumed to be non-zero, which is a contradiction.
We have obtained a return module of rank
$\ell $
for any set of cochains
$\alpha _i$
whose cohomology classes form a basis for
$\check H^1(\Omega , \mathbb {Q})$
and for almost every set of vectors
$w_i$
in a neighborhood of zero. This was done for a particular starting set of tile shapes, but the same argument works for any starting set. As a result, the set of shape classes for which all return modules have rank
$\ell $
or greater has full measure in the
$\ell d$
-dimensional space of possible shape classes.
Note that prior to the last paragraph, the proof never used the assumption that the dimension of
$\check H^1(\Omega _T, \mathbb {Q})$
was
$\ell $
. It merely used the existence of
$\ell $
linearly independent cohomology classes represented by closed PE cochains
$c_1, \ldots , c_\ell $
. If
$\check H^1(\Omega _T, \mathbb {Q})$
is infinite-dimensional, then we can find such a set of classes (and cochains) for any positive integer
$\ell $
. A shape change using generic shape classes in
$\check H^1_\ell \otimes \mathbb {Q}$
, where
$\check H^1_\ell $
is the span of the cohomology classes of the
$\alpha _i$
cochains, will then give us return modules of rank at least
$\ell $
. This justifies the comment after the statement of Corollary 1.3.
5 Examples
5.1 One-dimensional examples
Example 5.1. (Fibonacci)
The Fibonacci tiling is based on the substitution
$a \to ab$
,
${b \to a}$
. The first cohomology of the resulting tiling space has rank 2:
$\check H^1(\Omega ) = \hspace {0.5pt}\mathbb {Z}^2$
. Let
$P_0$
be a one-tile patch consisting of an a tile. The distance from each
$P_0$
to the subsequent
$P_0$
is either the length of an a tile (if the two
$P_0$
patches are back-to-back, as in
$aa$
) or the length of an a tile plus the length of a b tile (if the two
$P_0$
patches are separated by a b, as in
$aba$
). This means that
$\mathrm {Ret}(P_0)$
is the span of the length of an a tile and the length of a b tile. This has rank 1 if the ratio of the two lengths is rational and has rank 2 if the ratio is irrational.
What about bigger patches? Every large patch P must contain a supertile
$P_1$
of some order m and must be contained in some supertile
$P_2$
of order M. This means that we must have
$$ \begin{align*} \mathrm{Ret}(P_2) \subset \mathrm{Ret}(P) \subset \mathrm{Ret}(P_1). \end{align*} $$
However,
$\mathrm {Ret}(P_1)$
and
$\mathrm {Ret}(P_2)$
are the spans of the lengths of the two kinds of supertiles of order m and M, respectively. Since the substitution matrix
$ ( \begin {smallmatrix} 1 & 1 \cr 1 & 0 \end {smallmatrix} )$
is invertible over
$\hspace {0.5pt}\mathbb {Z}$
, having determinant
$-1$
, both of these are the same as the span of the lengths of the a and b tiles. In other words, all patches P have exactly the same return module as
$P_0$
and, in particular, have the same rank: 1 if
$|a|/|b| \in \mathbb {Q}$
and 2 if
$|a|/|b| \not \in \mathbb {Q}$
.
Note how these results fit with the general scheme of Theorems 1.1 and 1.2. The cohomology has rank 2, so the limiting rank cannot exceed 2. The limiting rank (and indeed, the rank of all patches) equals 2 unless the ratio
$|a|/|b|$
lies in a countable union of codimension-1 subsets of
$\mathbb {R}$
, namely the rational numbers
$\mathbb {Q}$
.
Changes in the lengths of a and b that preserve the average tile length
$\phi ^{-1} |a| + \phi ^{-2}|b|$
are actually topological conjugacies. This shows that a topological conjugacy of tiling spaces can change the limiting rank of the return modules, in this case, from 1 to 2 or vice versa.
So far, we have only considered versions of the Fibonacci tiling where all a tiles have length
$|a|$
and all b tiles have length
$|b|$
. We could also describe the Fibonacci tiling using collared tiles, with several different varieties of a tile, each with its own length, and several different varieties of b tile. The return module of small patches could then have rank greater than 2. For instance, the return vectors for vertices of arbitrary type are spanned by the lengths of all the different collared tiles. By collaring to a big enough radius and picking tile lengths that are rationally independent, we can get this rank to be as large as we wish. However, the limiting rank of the return modules can only be 1 or 2.
Incidentally, every Fibonacci tiling space obtained by collaring and varying the lengths of the collared tiles turns out to be MLD to a Fibonacci tiling space involving uncollared tiles. This is because two shape classes in the same cohomology class give rise to MLD tilings and because the generators of
$\check H^1(\Omega )$
can be expressed in terms of uncollared tiles. As noted earlier, tilings that are MLD have the same limiting ranks of return modules, but do not necessarily have the same ranks for small patches.
Example 5.2. (Sturmian tilings)
Our analysis of the Fibonacci tiling relied on its substitutive structure, but it is possible to derive similar results for any Sturmian tiling. A Sturmian tiling (see e.g., [Reference Arnoux, Pytheas Fogg, Berthé, Ferenczi, Mauduit and Siegel2]) is a canonical cut-and-project tiling from two dimensions to one. There are two kinds of tiles, which we call a and b, with the ratio of frequencies being an irrational number
$\alpha $
. Such a tiling can be described via a substitution if and only if
$\alpha $
is a quadratic irrational. The Fibonacci tiling is the simplest such case, with
$\alpha $
being the golden ratio
$\phi = (1+\sqrt {5})/2$
.
The first cohomology of any Sturmian tiling space is
$\hspace {0.5pt}\mathbb {Z}^2$
, with generators that count a and b tiles, respectively. As with the Fibonacci tiling, the return module for the smallest possible patch (a single tile) is generated by the lengths of the two tiles. This has rank 1 if
$|a|/|b|$
is rational and rank 2 if
$|a|/|b|$
is irrational. If we collar the Sturmian tiling and vary the lengths of the collared tiles, we can get the return modules of small patches to have arbitrarily large rank, but the return modules of large patches always have rank 2 for generic choices of the lengths of the a and b tiles, and rank 1 for countably many values of
$|a|/|b|$
.
Example 5.3. (Thue–Morse)
The Thue–Morse tiling is based on the substitution
$a \to ab$
,
$b \to ba$
. Note that both kinds of supertiles have one a tile and one b tile. No matter what lengths we assign to the basic tiles, all 1-supertiles have the same length
$|a|+|b|$
.
Any patch P of length 5 or greater must have two consecutive letters of the same type, as the patterns
$ababa$
and
$babab$
never appear. However,
$aa$
or
$bb$
can only appear when there is a supertile boundary in between the two a tiles or two b tiles. As a result, there is a unique way to group the tiles in P into supertiles. This implies that any return vector between two instances of P must be a multiple of
$|a|+|b|$
, and hence that
$\mathrm {Ret}(P)$
is an infinite cyclic group.
Note that
$\mathrm {Ret}(P)$
is not necessarily all of
$(|a|+|b|)\hspace {0.5pt}\mathbb {Z}$
. If P is long enough to determine the locations of the order-n supertiles, then
$\mathrm {Ret}(P)$
is actually contained in
$2^{n-1}(|a|+|b|)\hspace {0.5pt}\mathbb {Z}$
. However, this does not affect the rank of
$\mathrm {Ret}(P)$
, which is 1 for all P of length 5 or greater.
At first glance, this result is surprising, since the rank of
$\check H^1(\Omega ) = \hspace {0.5pt}\mathbb {Z}[1/2] \oplus \hspace {0.5pt}\mathbb {Z}$
is 2, not 1. Theorem 1.2 says that a generic shape change should result in return modules that have rank 2.
The answer is that part of the cohomology involves collared tiles and cannot be expressed in terms of the basic uncollared tiles. As we will soon see, a generic shape change among collared tiles does indeed result in a limiting rank of 2.
Since the patterns
$aaa$
and
$bbb$
never appear, there are six possible once-collared tiles:
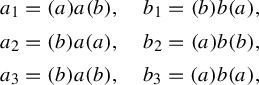$$ \begin{align*} a_1 &= (a)a(b), \quad b_1 = (b)b(a), \\ a_2 & = (b)a(a), \quad b_2 = (a)b(b), \\ a_3 & = (b)a(b), \quad b_3 = (a)b(a), \end{align*} $$
where
$(x)y(z)$
denotes a y tile that is preceded by an x tile and followed by a z tile.
The Anderson–Putnam complex that describes possible adjacencies between tiles is shown in Figure 3.
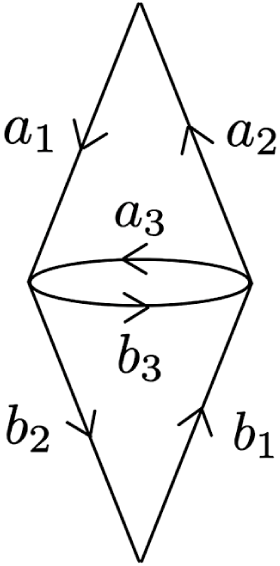
Figure 3 The Anderson–Putnam complex for the once-collared Thue–Morse substitution.
A path between two instances of a tile defines a closed loop in this complex, so the length of an arbitrary return vector is an integer combination of
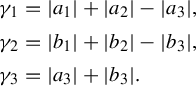$$ \begin{align*} \gamma_1 &= |a_1| + |a_2| - |a_3|, \\ \gamma_2 &= |b_1| + |b_2| - |b_3|, \\ \gamma_3 &= |a_3| + |b_3|. \end{align*} $$
The quantities
$\{\gamma _1, \gamma _2, \gamma _3\}$
are rationally independent given generic choices of tile lengths, so the return module for individual collared tiles generically has rank 3.
However, return modules for larger patches involve closed loops in an analogous complex built from supertiles, not just from individual tiles. Substitution sends
$\gamma _1$
and
$\gamma _2$
to
$\gamma _3$
and sends
$\gamma _3$
to
$\gamma _1+\gamma _2+\gamma _3$
, so the return vector for any patch containing a well-defined collared supertile is a combination of
$\gamma _1+\gamma _2$
and
$\gamma _3$
. The quantities
$\gamma _1+\gamma _2$
and
$\gamma _3$
transform under additional substitution via the matrix
$ ( \begin {smallmatrix} 0 & 1 \cr 2 & 1 \end {smallmatrix} )$
. This is invertible over
$\mathbb {Q}$
, so the rank of the return module for a high-order supertile is the same as the rank for an order-1 supertile. As a result, the limiting rank is at most 2 and is generically equal to 2.
Example 5.4. (Three-e Morse)
Our final one-dimensional (1D) example is a generalization of Thue–Morse that we call Three-e–Morse. Consider the substitution
$a \to aab$
,
${b \to bba}$
. This has features similar to both Thue–Morse and to the period-doubling substitution
${a \to ab}$
,
$b \to aa$
, only with a stretching factor of 3 instead of 2.
Working with basic tiles, there are only two lengths to play with, so the return module of a patch cannot have rank greater than 2. The substitution matrix
$ (\! \begin {smallmatrix} 2 & 1 \cr 1 & 2 \end {smallmatrix}\! )$
is invertible over
$\mathbb {Q}$
, so the rank of the return module of a high-order supertile (or of any patch found within a high-order supertile, in other words, of any patch at all) has the same rank as the return module of a simple tile. This rank is 1 if
$|a|/|b| \in \mathbb {Q}$
and 2 if
$|a|/|b| \not \in \mathbb {Q}$
.
However, the rank of
$\check H^1(\Omega ) = \hspace {0.5pt}\mathbb {Z}[1/3] \oplus \hspace {0.5pt}\mathbb {Z}^2$
is 3, not 2, so a generic shape change should give us rank-3 return modules. As with the Thue–Morse tiling, part of the cohomology is invisible to uncollared tiles, so we need to use collared tiles to achieve this. There are now eight collared tiles:
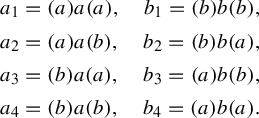$$ \begin{align*} a_1 &= (a)a(a), \quad b_1 = (b)b(b), \\ a_2 &= (a)a(b), \quad b_2 = (b)b(a), \\ a_3 &= (b)a(a), \quad b_3 = (a)b(b), \\ a_4 &= (b)a(b), \quad b_4 = (a)b(a). \end{align*} $$
The resulting Anderson–Putnam complex is shown in Figure 4.
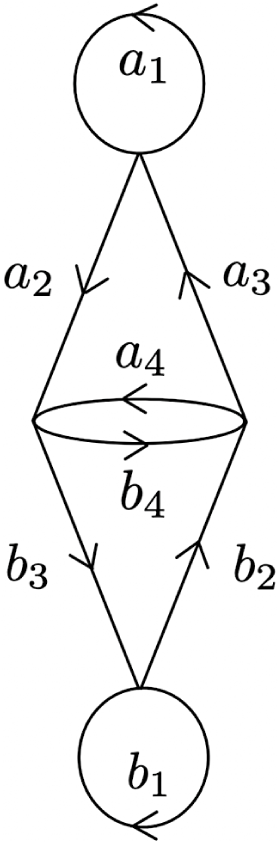
Figure 4 The Anderson–Putnam complex for the once-collared Three-e Morse tiling.
We define the quantities
$$ \begin{align*} \gamma_1 &= |a_1|, \\ \gamma_2 & = |b_1|, \\ \gamma_3 &= |a_2| + |a_3| - |a_4|, \\ \gamma_4 &= |b_3| + |b_3| - |b_4|, \\ \gamma_5 & = |a_4| + |b_4|. \end{align*} $$
By picking generic tile lengths, we can get the
$\gamma _i$
quantities to be rationally independent, so the rank of the return module of a single tile may have rank up to 5. Under substitution, the quantities
$\gamma _1, \ldots , \gamma _5$
transform via the matrix
$$ \begin{align*} \begin{pmatrix} 0&0&0&0&1 \cr 0&0&0&0&1 \cr 1 &0&1&0&1 \cr 0 & 1 & 0 & 1 & 1 \cr 1&1&1&1&1 \end{pmatrix}. \end{align*} $$
This matrix has rank 3, with eigenvalues 3, 1, -1, 0, and 0. Thus, the return module for order-1 supertiles (or for higher-order supertiles, or for any large patch) will generically have rank 3. If the
$\gamma _i$
quantities are not rationally independent, the rank may be even less.
The lesson in all of these examples is that the rank of the cohomology gives an upper bound on the limiting rank of return modules and gives the limiting rank exactly for a generic choice of tile lengths. If the cohomology can be expressed entirely using uncollared tiles, as in the Fibonacci tiling and other Sturmian tilings, then we only need to vary the lengths of the uncollared tiles to achieve this. If part of the cohomology can only be expressed using collared tiles, as in the Thue–Morse and Three-e–Morse tilings, then we need to vary the lengths of collared tiles to achieve generic behavior. In all cases, we can get return modules of small patches to be as complicated as we want by collaring and varying a large number of tile lengths. However, these complications disappear when we look at large patches, typically via the action of a singular substitution matrix.
5.2 Higher dimensional examples
When it comes to return modules, there are several key differences between the geometry of
$\mathbb {R}$
and that of
$\mathbb {R}^d$
with
$d>1$
. First, the return module of a repetitive tiling in d dimensions always has rank at least d. Since every ball of sufficient radius contains a copy of the patch P that we are studying, the real span of the return vectors of P is all of
$\mathbb {R}^d$
, so there must be d return vectors that are linearly independent over
$\mathbb {R}$
, and thus over
$\mathbb {Q}$
.
Second, non-generic behavior is rarer in higher dimensions than in one dimension, in the sense that it occurs on countably many copies of a codimension-d set instead of a codimension-1 set. (However, the word ‘rarer’ should be taken with a grain of salt, since in both cases, the sets have measure zero.) There are only countably many ways to have a rational linear relation among return vectors. Each such relation reduces the number of free vectors by one, thereby constraining us to a codimension-d subset of our set of possible shape parameters.
Finally, the maximal rank of a return module is the rank of
$\check H^1$
, but the dimension of the space of shape parameters is d times the rank of
$\check H^1$
. There are many, many more ways to vary the shapes and sizes of our tiles than there are generators of our return modules.
Example 5.5. (Chair)
There are two common versions of the chair tiling, each MLD to the other. In one, the basic tiles are an L-shaped triomino and rotations of that triomino by multiples of 90 degrees. The substitution rule for one tile is given in the top portion of Figure 5. To substitute rotated versions of the tile, just rotate the picture. In the other version of the chair tiling, a basic tile is a unit square marked with an arrow pointing northeast, northwest, southwest, or southeast. The substitution rule for arrow tiles is shown in the bottom portion of Figure 5. To go from chairs to arrows, divide each chair-shaped tile into three squares and draw arrows pointing toward the center. To go from arrows to chairs, look for vertices with three arrows pointing in and one pointing out. Glue the three squares with arrows pointing in to form a chair.
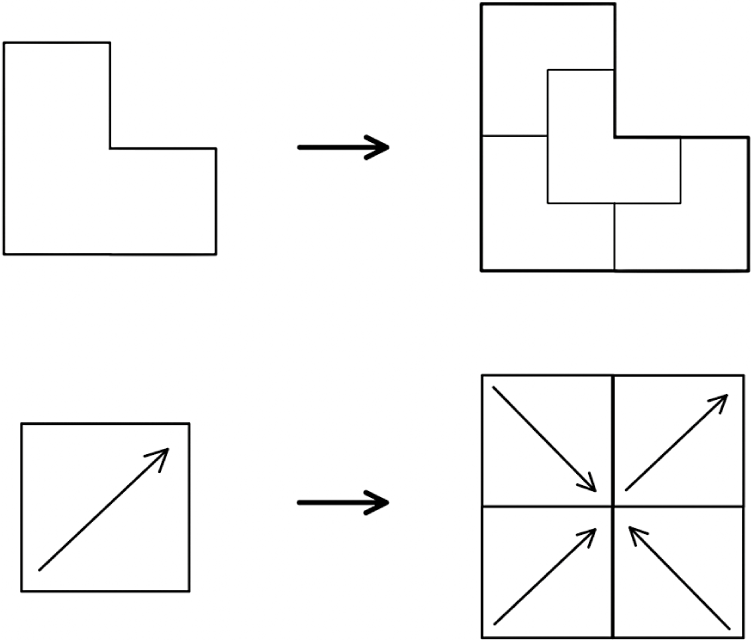
Figure 5 Substitutions for the classic and arrow versions of the chair tiling.
In either version, all of the vertices have exactly the same x-coordinate (mod 1) and the same y-coordinate (mod 1). The return module for any patch is necessarily a subgroup of
$\hspace {0.5pt}\mathbb {Z}^2$
and so has rank at most 2. (Depending on the size of the patch, the return module is typically
$2^n \hspace {0.5pt}\mathbb {Z}^2$
for some integer n.) The chair tiling, like all primitive substitution tilings, is repetitive, meaning that for each patch P, there is a radius
$r_P$
such that every ball of radius
$r_P$
contains at least one copy of P. This implies that the rank of
$\mathrm {Ret}(P)$
is at least equal to the dimension of the ambient space, in this case, 2. Remarkably, it is no bigger.
It is reasonable to wonder whether that rank can be increased by applying a shape change. For small patches the answer is ‘yes’, just as in our 1D examples. However, for large patches, the answer is ‘no’. Here,
$\check H^1(\Omega ) = \hspace {0.5pt}\mathbb {Z}[1/2]^2$
, which only has rank 2. By Theorem 1.1, no matter how we change the shapes, the limiting rank is at most 2. That is, the locations of every patch P above a certain size must live on a lattice, up to an overall translation.
Another perspective on this comes from the classification of shape changes up to MLD equivalence by
$\check H^1(\Omega , \mathbb {R}^2)$
[Reference Clark and Sadun6]. There is a 4-parameter family of rigid linear transformations that can be applied to the chair tiling. Since
$\check H^1(\Omega , \mathbb {R}^2) = \hspace {0.5pt}\mathbb {Z}[1/2]^2 \otimes \mathbb {R}^2 = \mathbb {R}^4$
is four-dimensional, all shape changes are MLD to rigid linear transformations, and in particular respect any lattice structure on any length scale larger than that of the MLD equivalence.
Example 5.6. (Hat)
In 2023, Smith et al [Reference Smith, Myers, Kaplan and Goodman-Strauss17] announced the discovery of a family of aperiodic monotiles. Each element in the family is a shape that, together with rotated and reflected versions of itself, can tile the plane but only non-periodically. Each tiling actually involves 12 tiles up to translation: the original shape rotated by multiples of 60 degrees and the reflected shape rotated by multiples of 60 degrees. (The same authors later displayed an aperiodic monotile called the Spectre [Reference Smith, Myers, Kaplan and Goodman-Strauss18] that uses 12 rotations and no reflections. We will not concern ourselves with the Spectre tilings here.)
The basic tile, shown in Figure 6, is a degenerate 14-gon, with six edges of length
$\alpha $
(shown as solid lines) and eight edges of length
$\beta $
(shown as dashed lines), and with two of the dashed edges laid end-to-end, looking like a single edge of length
$2\beta $
. The construction works for all positive values of
$\alpha $
and
$\beta $
, although some care must be taken with the special case
$\alpha =\beta $
(to ensure that
$\alpha $
edges cannot abut
$\beta $
edges) and with the limiting cases
$\alpha =0$
and
$\beta =0$
(to ensure that the zero-length edges still line up). Several special cases have been given names:
$\beta =0$
is a ‘Chevron’,
$\alpha /\beta =\sqrt {3}$
is a ‘Hat’,
$\alpha =\beta $
is a ‘Spectre’,
$\alpha /\beta =\sqrt {3}/3$
is a ‘Turtle’, and
$\alpha =0$
is a ‘Comet’. See Figure 7.
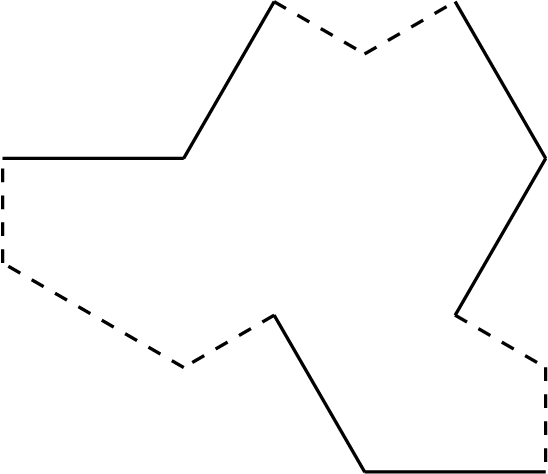
Figure 6 The basic ‘Hat’ tile. The lengths
$\alpha , \beta $
of the solid and dashed edges are arbitrary.
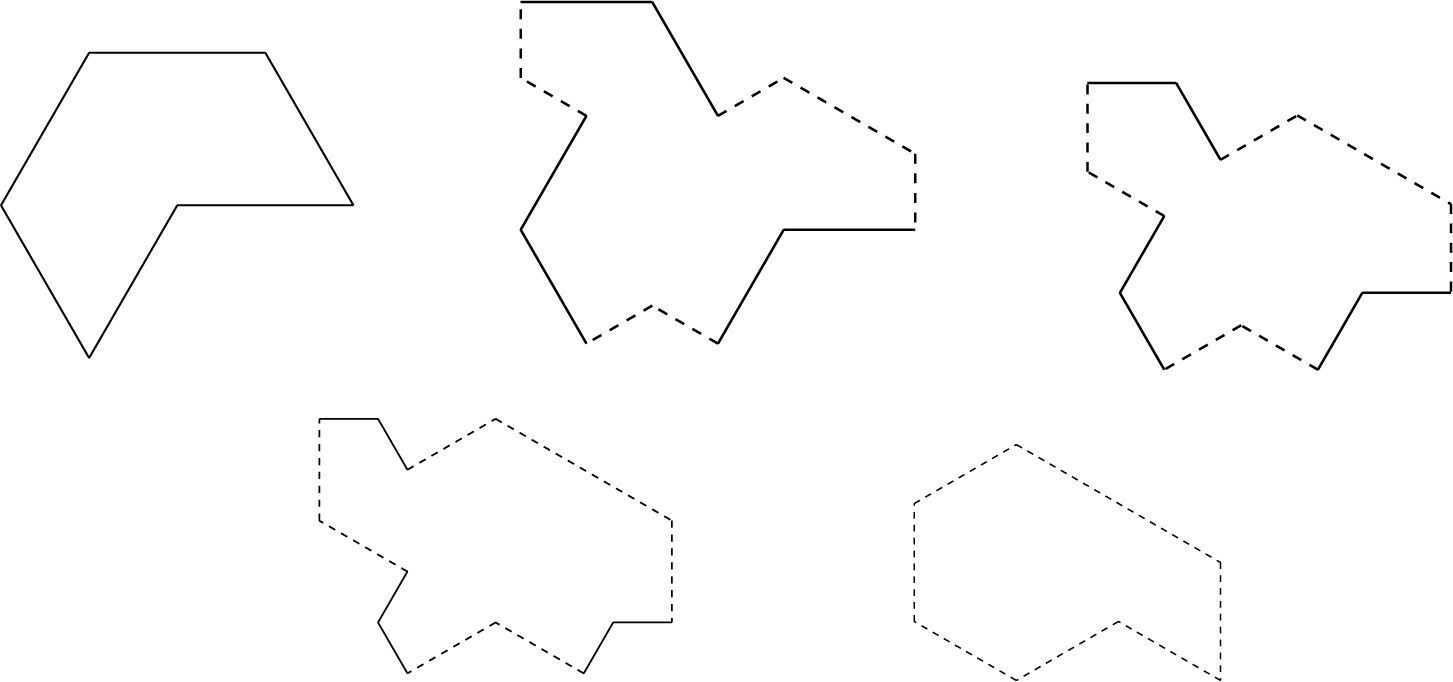
Figure 7 The Chevron, Hat, Spectre, Turtle, and Comet tiles, all rotated by 180 degrees.
In all cases, tiles must assemble into four shapes called ‘metatiles’. The metatiles then assemble into larger metatiles, which assemble into larger metatiles, and so on to infinity. The substitution involving metatiles has an overall stretching factor of
$\phi ^4$
, where
$\phi $
is the golden mean. Since
$\phi ^4$
is a unimodular Pisot number, this implies that the return module for high-order metatiles (and other large patches) is the same as for basic metatiles, just like what we saw with the Fibonacci tiling. We refer to this as the return module of the tiling. While it is possible to investigate the (possibly larger) return module for individual tiles, we will not do so.
The cohomology and return modules for tilings in the Hat family were computed in [Reference Baake, Gähler and Sadun3]. Here,
$\check H^1(\Omega )=\hspace {0.5pt}\mathbb {Z}^4$
, so the biggest rank the return module can have is 4. Our ambient space is two-dimensional, so the return module must have rank at least 2. Six-fold rotational symmetry implies that the rank of the return module must be even. In short, the rank must always be 2 or 4.
If we identify
$\mathbb {R}^2$
with the complex numbers
$\mathbb {C}$
, then the return module is closely related to the triangular lattice
$\hspace {0.5pt}\mathbb {Z}[\xi ]$
spanned by 1 and
$\xi = \exp (2\pi i/6) = (1 + i \sqrt {3})/2$
. Specifically, the return lattice is the span of
$(\alpha +i\beta ) (1+\xi ) \hspace {0.5pt}\mathbb {Z}[\xi ]$
and
$2i\beta (1+\xi ) \hspace {0.5pt}\mathbb {Z}[\xi ]$
. This has rank 2 if a rational multiple of
$2i\beta /\alpha $
lies in
$\hspace {0.5pt}\mathbb {Z}[\xi ]$
and rank 4 if it does not. Since the pure imaginary elements of
$\hspace {0.5pt}\mathbb {Z}[\xi ]$
are the multiples of
$i \sqrt {3}$
, the return module has rank 2 if and only if
$\beta \sqrt {3}/\alpha $
is rational or
$\alpha =0$
.
The upshot is that almost every shape in the Hat family results in a four-dimensional return module. However, four of the five named variants have two-dimensional return modules. In two of these, namely the Chevron and the Comet, all vertices lie on a triangular lattice, so the return module is necessarily contained in that lattice. In two others, namely the Hat and the Turtle, all vertices either lie on a triangular lattice or on its dual honeycomb grid.
So far, we have only considered the shapes discussed in [Reference Smith, Myers, Kaplan and Goodman-Strauss17], all of which respect 6-fold rotational symmetry and reflectional symmetry. In [Reference Baake, Gähler and Sadun3], the authors considered shape changes that broke reflectional symmetry while preserving rotational symmetry, resulting in two distinct shapes, each appearing in six orientations. This was done by allowing the parameters
$\alpha $
and
$\beta $
to be complex. As before, the return module has rank 2 exactly when
$i \beta /\alpha \in \mathbb {Q}[\xi ]$
, the set of rational multiples of
$\hspace {0.5pt}\mathbb {Z}[\xi ]$
. The set
$\mathbb {Q}[\xi ]$
is countable and dense in
$\mathbb {C}$
. Our space of shape parameters
$(\alpha , \beta )$
is
$\mathbb {C}^2 =\mathbb {R}^4$
, most of which give rise to rank-4 return modules. Only when
$(\alpha , \beta )$
lie in a countable union of two-dimensional subsets do we get rank 2.
Expanding our horizons further, we can consider shape changes that break 6-fold rotational symmetry. The space of possible shapes (up to MLD equivalence) is parameterized by
$\check H^1(\Omega ,\mathbb {R}^2) = \hspace {0.5pt}\mathbb {Z}^4 \otimes \mathbb {R}^2 = \mathbb {R}^8$
. Within this eight-dimensional space, the return module has rank 4 everywhere except on a countable union of six-dimensional subsets, where it can have rank 2 or 3.
Acknowledgements
It is our pleasure to thank Michael Baake, Franz Gähler, and Jianlong Liu for useful discussions. This work was supported by the National Science Foundation under grant DMS-2113468.
Open access
