Refine search
Actions for selected content:
7 results
On the smoothness of slowly varying functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 876-891
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On q-scale functions of spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 56-84
- Print publication:
- March 2023
-
- Article
- Export citation
SMOOTHNESS IN PENCILS OF HYPERSURFACES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 85-94
- Print publication:
- February 2023
-
- Article
- Export citation
Ruin probabilities with investments: smoothness, inegro-differential and ordinary differential equations, asymptotic behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 June 2022, pp. 556-570
- Print publication:
- June 2022
-
- Article
- Export citation
BIRKHOFF ORTHOGONALITY IN CLASSICAL
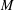 $M$ -IDEALS
$M$ -IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 279-288
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Smoothness in Relative Geometry
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 November 2013, pp. 461-491
- Print publication:
- December 2013
-
- Article
- Export citation
Uniform Mazur's Intersection Property of Balls
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 4 / 01 December 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 455-460
- Print publication:
- 01 December 1987
-
- Article
-
- You have access
- Export citation
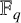
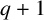
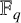
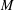
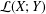
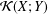
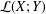
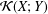
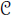 ⊗1). In this article, we define a notion of smoothness in this relative (and not necessarily additive) context which generalizes the notion of smoothness in the category of rings. This generalisation consists in replacing homological finiteness conditions by homotopical ones, using the Dold-Kan correspondence. To do this, we provide the category
⊗1). In this article, we define a notion of smoothness in this relative (and not necessarily additive) context which generalizes the notion of smoothness in the category of rings. This generalisation consists in replacing homological finiteness conditions by homotopical ones, using the Dold-Kan correspondence. To do this, we provide the category 