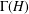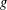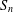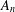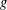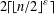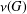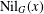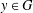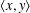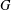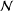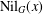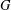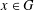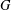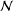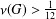Refine search
Actions for selected content:
4 results
ON THE GENERATING GRAPH OF A SIMPLE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 91-103
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
FINDING INVOLUTIONS WITH SMALL SUPPORT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 43-47
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
FACTORIZATION NUMBERS OF SOME FINITE GROUPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 2 / May 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 345-354
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation