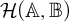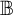Refine search
Actions for selected content:
3 results
Ultrafilters in the random real model
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-25
-
- Article
- Export citation
ON SEQUENCES OF HOMOMORPHISMS INTO MEASURE ALGEBRAS AND THE EFIMOV PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 191-218
- Print publication:
- March 2023
-
- Article
- Export citation
Can Mean Helicity Fluctuations Explain the Variability of the Solar Cycle ?
-
- Journal:
- Symposium - International Astronomical Union / Volume 157 / 1993
- Published online by Cambridge University Press:
- 19 July 2016, pp. 71-75
- Print publication:
- 1993
-
- Article
-
- You have access
- Export citation