Hostname: page-component-5cf477f64f-fcbfl Total loading time: 0 Render date: 2025-04-04T06:26:26.331Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SEQUENCES OF HOMOMORPHISMS INTO MEASURE ALGEBRAS AND THE EFIMOV PROBLEM

Part of: Set theory Miscellaneous topics in measure theory Classical measure theory

Published online by Cambridge University Press:  13 September 2021

PIOTR BORODULIN–NADZIEJA  and
DAMIAN SOBOTA
PIOTR BORODULIN–NADZIEJA
Affiliation:
INSTYTUT MATEMATYCZNY UNIWERSYTET WROCŁAWSKI PL. GRUNWALDZKI 2/4, 50-384 WROCŁAW, POLAND E-mail: pborod@math.uni.wroc.pl
DAMIAN SOBOTA*
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC DEPARTMENT OF MATHEMATICS UNIVERSITY OF VIENNA KOLINGASSE 14-16, 1090 VIENNA, AUSTRIA
*
E-mail: damian.sobota@univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

For given Boolean algebras 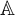$\mathbb {A}$ and 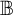$\mathbb {B}$ we endow the space 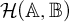$\mathcal {H}(\mathbb {A},\mathbb {B})$ of all Boolean homomorphisms from 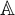$\mathbb {A}$ to 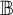$\mathbb {B}$ with various topologies and study convergence properties of sequences in 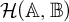$\mathcal {H}(\mathbb {A},\mathbb {B})$ . We are in particular interested in the situation when 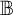$\mathbb {B}$ is a measure algebra as in this case we obtain a natural tool for studying topological convergence properties of sequences of ultrafilters on 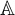$\mathbb {A}$ in random extensions of the set-theoretical universe. This appears to have strong connections with Dow and Fremlin’s result stating that there are Efimov spaces in the random model. We also investigate relations between topologies on 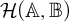$\mathcal {H}(\mathbb {A},\mathbb {B})$ for a Boolean algebra 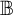$\mathbb {B}$ carrying a strictly positive measure and convergence properties of sequences of measures on 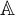$\mathbb {A}$ .

Keywords

Efimov problemmeasure algebrasweak convergence of measuresalgebraic convergencerandom forcingperfect Hamming codes

MSC classification

Primary: 28A20: Measurable and nonmeasurable functions, sequences of measurable functions, modes of convergence
Secondary: 28A60: Measures on Boolean rings, measure algebras 03E40: Other aspects of forcing and Boolean-valued models 28E15: Other connections with logic and set theory 03E75: Applications of set theory 28A33: Spaces of measures, convergence of measures
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 1 , March 2023 , pp. 191 - 218
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assmus, E. F. Jr. and Key, J. D., Designs and Their Codes , Cambridge Tracts in Mathematics, vol. 103, Cambridge University Press, Cambridge, 1992.CrossRefGoogle Scholar
Balcar, B., Franěk, F., and Hruška, J., Exhaustive zero-convergence structures on Boolean algebras . Acta Universitatis Carolinae, Mathematica et Physica , vol. 40 (1999), pp. 27–41.Google Scholar
Balcar, B., Główczyński, W., and Jech, T., The sequential topology on complete Boolean algebras . Fundamenta Mathematicae , vol. 155 (1998), no. 1, pp. 59–78.Google Scholar
Borodulin-Nadzieja, P. and Cegiełka, K., Homomorphisms, measures and forcing names for ultrafilters, preprint.Google Scholar
Brian, W. and Dow, A., Small cardinals and small Efimov spaces . Annals of Pure and Applied Logic , vol. 173 (2022), p. 103043.CrossRefGoogle Scholar
Diestel, J., Sequences and Series in Banach Spaces , Graduate Texts in Mathematics, vol. 92, Springer, New York, 1984.CrossRefGoogle Scholar
Dow, A. and Fremlin, D., Compact sets without converging sequences in the random real model . Acta Mathematica Universitatis Comenianae , vol. 76 (2007), no. 2, pp. 161–171.Google Scholar
Dow, A. and Pichardo-Mendoza, R., Efimov spaces, CH, and simple extensions . Topology Proceedings , vol. 33 (2009), pp. 277–283.Google Scholar
Dow, A. and Shelah, S., An Efimov space from Martin’s Axiom . The Houston Journal of Mathematics , vol. 39 (2013), no. 4, pp. 1423–1435.Google Scholar
Fedorčuk, V. V., Fully closed mappings and the consistency of some theorems of general topology with the axioms of set theory . Mathematics of the USSR-Sbornik , vol. 28 (1976), no. 1, pp. 1–26.CrossRefGoogle Scholar
Hamming, R. W., Error detecting and error correcting codes . The Bell System Technical Journal , vol. 29 (1950), pp. 147–160.Google Scholar
Hart, K. P., Efimov’s problem , Open Problems in Topology II (E. Pearl, editor), Elsevier Science, Amsterdam, 2007, pp. 171–177.CrossRefGoogle Scholar
Hrušák, M. and Shibakov, A., Convergent sequences in topological groups . Annals of Pure and Applied Logic , vol. 172 (2020), p. 102910.CrossRefGoogle Scholar
Jech, T., Convergence and submeasures in Boolean algebras . Commentationes Mathematicae Universitatis Carolinae , vol. 59 (2018), no. 4, pp. 503–511.Google Scholar
Kolmogorov, A. N., Complete metric Boolean algebras . Philosophical Studies , vol. 77 (1995), no. 1, pp. 57–66, translated from the French by Richard Jeffrey.CrossRefGoogle Scholar
Kopczyński, E. and Niwiński, D., A simple indeterminate infinite game , Logic, Computation, Hierarchies , Ontos Mathematical Logic, vol. 4, De Gruyter, Berlin, 2014, pp 205–211.CrossRefGoogle Scholar
Koszmider, P. and Shelah, S., Independent families in Boolean algebras with some separation properties . Algebra Universalis , vol. 69 (2013), no. 4, pp. 305–312.CrossRefGoogle Scholar
Seever, G. L., Measures on F-spaces . Transactions of the American Mathematical Society , vol. 133 (1968), pp. 267–280.Google Scholar
Sobota, D. and Zdomskyy, L., Convergence of measures in forcing extensions . Israel Journal of Mathematics , vol. 232 (2019), no. 2, pp. 501–529.CrossRefGoogle Scholar