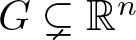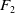Refine search
Actions for selected content:
8 results
Are free groups of different ranks bi-invariantly quasi-isometric?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 356-364
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Teichmüller displacement theorem on Gromov hyperbolic spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1148-1166
-
- Article
- Export citation
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
2 - Coarse Structure and Metrisability
-
- Book:
- Coarse Geometry of Topological Groups
- Published online:
- 16 December 2021
- Print publication:
- 16 December 2021, pp 19-67
-
- Chapter
- Export citation
INFINITE STRINGS AND THEIR LARGE SCALE PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 October 2020, pp. 585-625
- Print publication:
- June 2022
-
- Article
- Export citation
QUASICONFORMAL HARMONIC MAPPINGS BETWEEN DOMAINS CONTAINING INFINITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 109-117
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Rigidity Properties for Hyperbolic Generalizations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 November 2019, pp. 66-76
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation