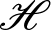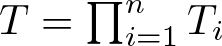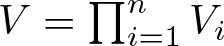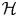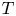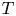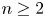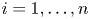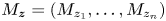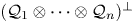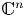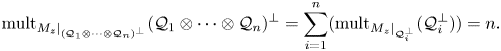Refine search
Actions for selected content:
7 results
Burns-Krantz rigidity in non-smooth domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1037-1046
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
TOTALLY NULL SETS FOR A(X)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 108-114
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Universal functions in several complex variables
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 2 / September 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-196
- Print publication:
- September 1979
-
- Article
-
- You have access
- Export citation
Inner functions and the maximal ideal space of L∞(Tn)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 2 / September 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-178
- Print publication:
- September 1978
-
- Article
-
- You have access
- Export citation