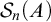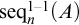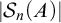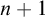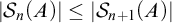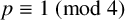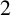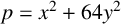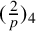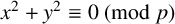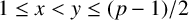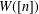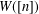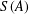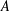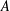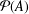Refine search
Actions for selected content:
27 results
PKLM: A Flexible MCAR Test Using Classification
-
- Journal:
- Psychometrika / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 January 2025, pp. 280-303
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Posterior Probabilities for a Consensus Ordering
-
- Journal:
- Psychometrika / Volume 55 / Issue 1 / March 1990
- Published online by Cambridge University Press:
- 01 January 2025, pp. 53-63
-
- Article
- Export citation
Extending Multivariate Distance Matrix Regression with an Effect Size Measure and the Asymptotic Null Distribution of the Test Statistic
-
- Journal:
- Psychometrika / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1052-1077
-
- Article
- Export citation
Resampling-Based Inference Methods for Comparing Two Coefficients Alpha
-
- Journal:
- Psychometrika / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 January 2025, pp. 203-222
-
- Article
- Export citation
Statistical Significance of the Contribution of Variables to the PCA solution: An Alternative Permutation Strategy
-
- Journal:
- Psychometrika / Volume 76 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 01 January 2025, pp. 440-460
-
- Article
- Export citation
A Multistage Ranking Model
-
- Journal:
- Psychometrika / Volume 65 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 01 January 2025, pp. 217-231
-
- Article
- Export citation
THE PERMUTATIONS WITH n NON-FIXED POINTS AND THE SEQUENCES WITH LENGTH n OF A SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 July 2022, pp. 1067-1076
- Print publication:
- September 2024
-
- Article
- Export citation
A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF
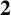 $\mathbf {2}$
$\mathbf {2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1-6
- Print publication:
- August 2022
-
- Article
- Export citation
6 - Loose Canons? Music and the Craft of Ecclesiastical Power
-
- Book:
- Music and Musicians at the Collegiate Church of St Omer
- Published online:
- 31 August 2020
- Print publication:
- 17 September 2020, pp 201-256
-
- Chapter
- Export citation
FACTORIALS OF INFINITE CARDINALS IN ZF PART I: ZF RESULTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 224-243
- Print publication:
- March 2020
-
- Article
- Export citation
FACTORIALS OF INFINITE CARDINALS IN ZF PART II: CONSISTENCY RESULTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 244-270
- Print publication:
- March 2020
-
- Article
- Export citation
DEGREE OF THE
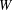 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Triangularization of Matrices and Polynomial Maps
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 September 2019, pp. 94-105
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Power and False Negatives in Qualitative Comparative Analysis: Foundations, Simulation and Estimation for Empirical Studies
-
- Journal:
- Political Analysis / Volume 26 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 29 January 2018, pp. 72-89
-
- Article
- Export citation
A FINITE-TO-ONE MAP FROM THE PERMUTATIONS ON A SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 177-182
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Number of Right Ideals and a q-analogue of Indecomposable Permutations
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 3 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-503
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Quantifying Randomness Versus Consensus in Wine Quality Ratings*
-
- Journal:
- Journal of Wine Economics / Volume 9 / Issue 2 / August 2014
- Published online by Cambridge University Press:
- 29 April 2014, pp. 202-213
-
- Article
- Export citation
On automatic infinite permutations∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 23 November 2011, pp. 77-85
- Print publication:
- January 2012
-
- Article
- Export citation
Matchmaking and Testing for Exponentiality in the M/G/∞ Queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-144
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation