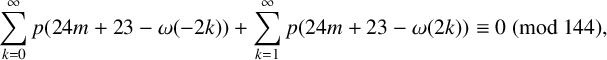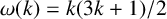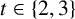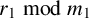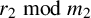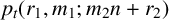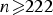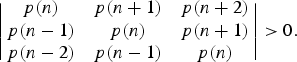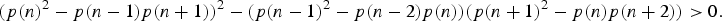Refine search
Actions for selected content:
17 results
Inequality arising from the iterated Laguerre operator for various partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-22
-
- Article
- Export citation
2 - Probability Theory
-
- Book:
- Statistical Mechanics for Physicists and Mathematicians
- Published online:
- 28 July 2025
- Print publication:
- 14 August 2025, pp 6-50
-
- Chapter
- Export citation
15 - The Path Integral
-
- Book:
- Quantum Mechanics
- Published online:
- 27 June 2025
- Print publication:
- 19 June 2025, pp 522-561
-
- Chapter
- Export citation
24 - Approximate tensor network contraction
- from Part II - Quantum algorithmic primitives
-
- Book:
- Quantum Algorithms
- Published online:
- 03 May 2025
- Print publication:
- 24 April 2025, pp 305-310
-
- Chapter
-
- You have access
- Open access
- Export citation
DIVISIBILITY OF SUMS OF PARTITION NUMBERS BY MULTIPLES OF 2 AND 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 271-279
- Print publication:
- October 2024
-
- Article
- Export citation
3 - Partial Summations and Effective Interactions
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 65-93
-
- Chapter
- Export citation
5 - The Onsager Solution and Exact Series Expansions
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 125-149
-
- Chapter
- Export citation
4 - Infinite Ising Systems in One Dimension
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 94-124
-
- Chapter
- Export citation
2 - Finite Ising Systems
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 29-64
-
- Chapter
- Export citation
1 - The Ising Model
-
- Book:
- A Student's Guide to the Ising Model
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023, pp 1-28
-
- Chapter
- Export citation

A Student's Guide to the Ising Model
-
- Published online:
- 11 May 2023
- Print publication:
- 25 May 2023
-
- Textbook
- Export citation
ON THE NUMBER OF 2-HOOKS AND 3-HOOKS OF INTEGER PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 18 August 2022, pp. 432-439
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - The Canonical Ensemble
-
- Book:
- Essential Statistical Physics
- Published online:
- 29 August 2020
- Print publication:
- 16 July 2020, pp 48-85
-
- Chapter
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
Shearer's point process, the hard-sphere model, and a continuum Lovász local lemma
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 1-23
- Print publication:
- March 2017
-
- Article
- Export citation
Directed polymer in random environment and last passage percolation*
-
- Journal:
- ESAIM: Probability and Statistics / Volume 14 / 2010
- Published online by Cambridge University Press:
- 29 October 2010, pp. 263-270
- Print publication:
- 2010
-
- Article
- Export citation
Exponential functionals of Brownian motion and disordered systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-271
- Print publication:
- June 1998
-
- Article
- Export citation