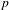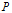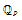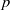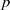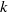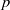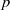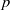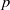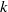Refine search
Actions for selected content:
4 results
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
RELATIVE UNITARY RZ-SPACES AND THE ARITHMETIC FUNDAMENTAL LEMMA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 March 2020, pp. 241-301
- Print publication:
- January 2022
-
- Article
- Export citation
Partial Hasse Invariants, Partial Degrees, and the Canonical Subgroup
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 4 / 01 August 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 742-772
- Print publication:
- 01 August 2018
-
- Article
-
- You have access
- Export citation
Random Dieudonné modules, random
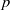 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 651-676
- Print publication:
- July 2013
-
- Article
- Export citation