Let $K$ be a number field with a ring of integers ${\mathcal{O}}$. We follow Ferraguti and Micheli [‘On the Mertens–Cèsaro theorem for number fields’, Bull. Aust. Math. Soc.93(2) (2016), 199–210] to define a density for subsets of ${\mathcal{O}}$ and use it to find the density of 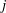the set of $j$-wise relatively $r$-prime $m$-tuples of algebraic integers. This provides a generalisation and analogue for several results on natural densities of integers and ideals of algebraic integers.

For $n=3$, $4$, and 5, we prove that, when $S_{n}$-number fields of degree $n$ are ordered by their absolute discriminants, the lattice shapes of the rings of integers in these fields become equidistributed in the space of lattices.

Let $K$ be a number field with ring of integers ${\mathcal{O}}$. After introducing a suitable notion of density for subsets of ${\mathcal{O}}$, generalising the natural density for subsets of $\mathbb{Z}$, we show that the density of the set of coprime $m$-tuples of algebraic integers is $1/{\it\zeta}_{K}(m)$, where ${\it\zeta}_{K}$ is the Dedekind zeta function of $K$. This generalises a result found independently by Mertens [‘Ueber einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338] and Cesàro [‘Question 75 (solution)’, Mathesis 3 (1883), 224–225] concerning the density of coprime pairs of integers in $\mathbb{Z}$.

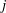
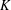
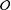
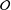
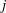
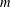
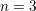
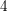
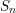
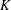
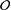
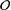
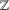
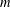
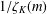
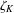
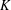
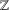
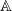Let be a commutative algebraic group defined over a number field 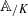K. For a prime ℘ in K where has good reduction, let N℘,n be the number of n-torsion points of the reduction of modulo ℘ where n is a positive integer. When is of dimension one and n is relatively prime to a fixed finite set of primes depending on , we determine the average values of N℘,n as the prime ℘ varies. This average value as a function of n always agrees with a divisor function.

A theorem of Kuyk says that every Abelian extension of a Hilbertian field is Hilbertian. We conjecture that for an Abelian variety A defined over a Hilbertian field K every extension L of K in K(Ator) is Hilbertian. We prove our conjecture when K is a number field. The proof applies a result of Serre about l-torsion of Abelian varieties, information about l-adic analytic groups, and Haran's diamond theorem.

We show that for the primes l = 2, 3, 5, 7 or 13, there do not exist any non-zero abelian varieties over $\mathbb{Q}$ that have good reduction at every prime different from l and are semi-stable at l. We show that any semi-stable abelian variety over $\mathbb{Q}$ with good reduction outside l = 11 is isogenous to a power of the Jacobian variety of the modular curve X0(11). In addition, we show that for l = 2, 3 and 5, there do not exist any non-zero abelian varieties over $\mathbb{Q}$ with good reduction outside l that acquire semi-stable reduction at l over a tamely ramified extension.

Convolution structures are group-like objects that were extensively studied by harmonic analysts. We use them to define H0 and H1 for Arakelov divisors over number fields. We prove the analogs of the Riemann–Roch and Serre duality theorems. This brings more structure to the works of Tate and van der Geer and Schoof. The H1 is defined by a procedure very similar to the usual Ĉech cohomology. Serre′s duality becomes Pontryagin duality of convolution structures. The whole theory is parallel to the geometric case.