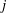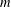Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fernández, José L.
and
Fernández, Pablo
2021.
Divisibility properties of random samples of integers.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 1,
Sittinger, Brian D.
and
Chen, Vickie V.
2024.
The density of tuples restricted by relativelyr-prime conditions.
Miskolc Mathematical Notes,
Vol. 25,
Issue. 1,
p.
465.