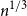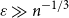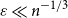Refine search
Actions for selected content:
2 results
Noise sensitivity on affine Weyl groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 31 July 2025, pp. 754-779
-
- Article
- Export citation
Noise sensitivity of the minimum spanning tree of the complete graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 708-723
-
- Article
-
- You have access
- Open access
- HTML
- Export citation