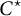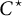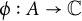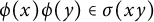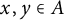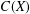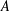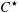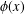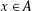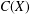Refine search
Actions for selected content:
3 results
Continuity and realization of multiplicative maps between RKHS and their cyclicity preserving properties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-14
-
- Article
- Export citation
A multiplicative Kowalski–Słodkowski theorem for
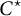 $C^\star $-algebras
$C^\star $-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 November 2022, pp. 951-958
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATIVE SPECTRAL FUNCTIONALS ON
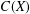 $C(X)$
$C(X)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 303-307
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation