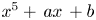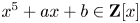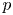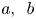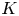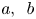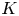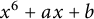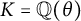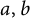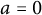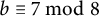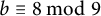Refine search
Actions for selected content:
4 results
MONOGENITY OF THE COMPOSITION OF POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 May 2025, pp. 1-9
-
- Article
- Export citation
NONMONOGENITY OF NUMBER FIELDS DEFINED BY TRUNCATED EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 497-504
- Print publication:
- June 2025
-
- Article
- Export citation
Common index divisor of the number fields defined by $x^5+\,ax\,+b$
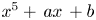
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 1147-1161
-
- Article
- Export citation
On nonmonogenic number fields defined by
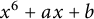 $x^6+ax+b$
$x^6+ax+b$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 788-794
- Print publication:
- September 2022
-
- Article
- Export citation