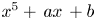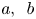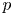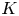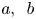Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ben Yakkou, H.
and
Boudine, B.
2023.
On the index of the octic number field defined by $x^8+ax+b$.
Acta Mathematica Hungarica,
Vol. 170,
Issue. 2,
p.
585.
Gaál, István
2024.
Monogenity and Power Integral Bases: Recent Developments.
Axioms,
Vol. 13,
Issue. 7,
p.
429.