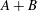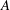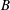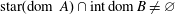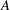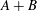Refine search
Actions for selected content:
3 results
The range of the Douglas–Rachford operator in infinite-dimensional Hilbert spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-18
-
- Article
- Export citation
On Bauschke–Bendit–Moursi modulus of averagedness and classifications of averaged nonexpansive operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation