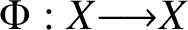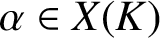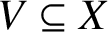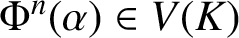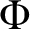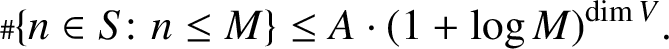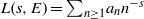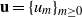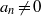Refine search
Actions for selected content:
4 results
Multiplicative dependence in linear recurrence sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1278-1288
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 23 February 2021, pp. 381-390
- Print publication:
- December 2021
-
- Article
- Export citation
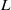 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
The Number of Solutions of Polynomial-Exponential Equations
-
- Journal:
- Compositio Mathematica / Volume 120 / Issue 2 / January 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 193-225
- Print publication:
- January 2000
-
- Article
-
- You have access
- Export citation