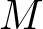Refine search
Actions for selected content:
1 results
Intrinsic stochastic differential equations and the extended Itô formula on manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
A general way to represent stochastic differential equations (SDEs) on smooth manifolds is based on the Schwartz morphism. In this manuscript, we are interested in SDEs on a smooth manifold
$M$ that are driven by p-dimensional Wiener process 
$W_t \in \mathbb{R}^p$ and time 
$t$. In terms of the Schwartz morphism, such an SDE is represented by a Schwartz morphism that morphs the semimartingale 
$(t,W_t)\in\mathbb{R}^{p+1}$ into a semimartingale on the manifold 
$M$. We show that it is possible to construct such Schwartz morphisms using special maps that we call diffusion generators. We show that one of the ways to construct a diffusion generator is by considering the flow of differential equations. One particular case is the construction of diffusion generators using Lagrangian vector fields. Using the diffusion generator approach, we also give the extended Itô formula (also known as generalized Itô formula or Itô–Wentzell formula) for SDEs on manifolds.
