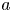Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 764-783
- Print publication:
- June 2023
-
- Article
- Export citation
-
We consider the following inhomogeneous problems
\begin{cases} \epsilon^{2}\mbox{div}(a(x)\nabla u(x))+f(x,u)=0 & \text{ in }\Omega,\\ \frac{\partial u}{\partial \nu}=0 & \text{ on }\partial \Omega,\\ \end{cases}where \Omega is a smooth and bounded domain in general dimensional space \mathbb {R}^{N}, \epsilon >0 is a small parameter and function a is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are L^{1}-local minimizer and global minimizer of the associated energy functional.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
