Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T09:03:13.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  08 March 2022

Zhuoran Du
Zhuoran Du*
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, PR China (duzr@hnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following inhomogeneous problems

\[ \begin{cases} \epsilon^{2}\mbox{div}(a(x)\nabla u(x))+f(x,u)=0 & \text{ in }\Omega,\\ \frac{\partial u}{\partial \nu}=0 & \text{ on }\partial \Omega,\\ \end{cases} \]
where $\Omega$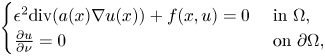 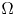is a smooth and bounded domain in general dimensional space $\mathbb {R}^{N}$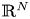, $\epsilon >0$ 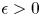is a small parameter and function $a$ 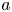is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are $L^{1}$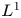-local minimizer and global minimizer of the associated energy functional.

Keywords

Local minimizerinterior transition layerinterface locationinhomogeneous transition problems

MSC classification

Primary: 35B25: Singular perturbations
Secondary: 35J20: Variational methods for second-order elliptic equations 35J61: Semilinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 764 - 783
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, S. and Ambrosetti, A.. A textbook on ordinary differential equations, 2nd Ed. (Switzerland: Springer International Publishing, 2015).Google Scholar
Alikakos, N. and Bates, P. W.. On the singular limit in a phase field model of phase transitions. Ann. Inst. H. Poincaré Anal. Non Linéaire 5 (1988), 141–178.CrossRefGoogle Scholar
Alikakos, N., Bates, P. W. and Chen, X.. Periodic traveling waves and locating oscillating patterns in multidimensional domains. Trans. Am. Math. Soc. 351 (1999), 2777–2805.CrossRefGoogle Scholar
Alikakos, N. and Simpson, H. C.. A variational approach for a class of singular perturbation problems and applications. Proc. R. Soc. Edinburgh Sect. A 107 (1987), 27–42.CrossRefGoogle Scholar
Allen, S. and Cahn, J. W.. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27 (1979), 1085–1095.CrossRefGoogle Scholar
Dancer, E. N. and Yan, S.. Multi-layer solutions for an elliptic problem. J. Differ. Eqns 194 (2003), 382–405.CrossRefGoogle Scholar
Dancer, E. N. and Yan, S.. Construction of various types of solutions for an elliptic problem. Calc. Var. Partial Differ. Equ. 20 (2004), 93–118.CrossRefGoogle Scholar
del Pino, M.. Layers with nonsmooth interface in a semilinear elliptic problem. Commun. Partial Differ. Equ. 17 (1992), 1695–1708.10.1080/03605309208820900CrossRefGoogle Scholar
del Pino, M.. Radially symmetric internal layers in a semilinear elliptic system. Trans. Am. Math. Soc. 347 (1995), 4807–4837.CrossRefGoogle Scholar
del Pino, M., Kowalczyk, M. and Wei, J.. Resonance and interior layers in an inhomogenous phase transition model. SIAM J. Math. Anal. 38 (2007), 1542–1564.CrossRefGoogle Scholar
Do Nascimento, A. S.. Stable transition layers in a semilinear diffusion equation with spatial inhomogeneities in $N$-dimensional domains. J. Differ. Eqns 190 (2003), 16–38.CrossRefGoogle Scholar
Do Nascimento, A. S. and Sônego, M.. The roles of diffusivity and curvature in patterns on surfaces of revolution. J. Math. Anal. Appl. 412 (2014), 1084–1096.CrossRefGoogle Scholar
Du, Z. and Gui, C.. Interior layers for an inhomogeneous Allen–Cahn equation. J. Differ. Eqns 249 (2010), 215–239.CrossRefGoogle Scholar
Du, Z., Gui, C., Sire, Y. and Wei, J.. Layered solutions for a fractional inhomogeneous Allen–Cahn equation. Nonlinear Differ. Equ. Appl. 23 (2016), 29.CrossRefGoogle Scholar
Du, Z. and Lai, B.. Transition layers for an inhomogeneous Allen–Cahn equation in Riemannian manifolds. Discrete Contin. Dyn. Syst., A 33 (2013), 1407–1429.CrossRefGoogle Scholar
Du, Z. and Wang, L.. Interface foliation for an inhomogeneous Allen–Cahn equation in Riemannian manifolds. Calc. Var. Partial Differ. Equ. 47 (2013), 343–381.CrossRefGoogle Scholar
Du, Z. and Wei, J.. Clustering layers for the Fife–Greenlee problem in $\mathbb {R}^{n}$. Proc. Royal Soc. Edinburgh A 146 (2016), 107–139.CrossRefGoogle Scholar
Fife, P. C. and Greenlee, W. M.. Interior transition layers for elliptic boundary value problems with a small parameter. Russ. Math. Surveys 29: 4 (1974), 103–131.CrossRefGoogle Scholar
Giusti, E.. Minimal surfaces and functions of bounded variation (Birkhäuser, Australia, 1984).CrossRefGoogle Scholar
Kohn, R. V. and Sternberg, P.. Local minimizers and singular perturbations. Proc. R. Soc. Edinburgh Sect. A 11 (1989), 69–84.CrossRefGoogle Scholar
Li, F. and Nakashima, K.. Transition layer for a spatially inhomogeneous Allen–Cahn equation in multi-dimensional domains. Discrete Contin. Dyn. Syst., A 32 (2012), 1391–1420.CrossRefGoogle Scholar
Mahmoudi, F., Malchiodi, A. and Wei, J.. Transition layer for the heterogeneous Allen–Cahn equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 25 (2008), 609–631.Google Scholar
Modica, L.. The gradient theory of phase transitions and the minimal interface criterion. Arch. Ration. Mech. Anal. 98 (1987), 123–142.CrossRefGoogle Scholar
Modica, L. and Mortola, S.. Un esempio di $\Gamma$-convergenza. Boll. Unione Mat. Ital. Sez. 14B (1977), 285–299.Google Scholar
Nakashima, Kimie. Stable transition layers in a balanced bistable equation. Differ. Integr. Equ. 13 (2000), 1025–1038.Google Scholar
Nakashima, Kimie. Multi-layered stationary solutions for a spatially inhomogeneous Allen–Cahn equation. J. Differ. Eqns 191 (2003), 234–276.CrossRefGoogle Scholar
Nakashima, K. and Tanaka, K.. Clustering layers and boundary layers in spatially inhomogenerous phase transition problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 20 (2003), 107–143.CrossRefGoogle Scholar
Sônego, M.. On the internal transition layer to some inhomogeneous semilinear problems: interface location. J. Math. Anal. Appl. 502 (2021), 125266.CrossRefGoogle Scholar
Sotomayor, J.. Liçōes de equaçōes diferenciais ordinárias (IMPA: Rio de Janeiro, 1979).Google Scholar
Sternberg, P.. The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. Anal. 101 (1988), 209–260.CrossRefGoogle Scholar
Wei, J. and Yang, J.. Toda system and cluster phase transitional layers in an inhomogeneous phase transitional model. Asympt. Anal. 69 (2010), 175–218.Google Scholar
Yang, J. and Yang, X.. Clustered interior phase transition layers for an inhomogeneous Allen–Cahn equation on higher dimensional domain. Commun. Pure Appl. Anal. 12 (2013), 303–340.CrossRefGoogle Scholar
Zúñiga, A. and Agudelo, O.. A two end family of solutions for the inhomogeneous Allen–Cahn equation in $\mathbb {R}^{2}$. J. Differ. Eqns 256 (2014), 157–205.CrossRefGoogle Scholar