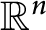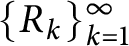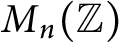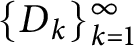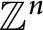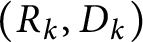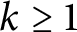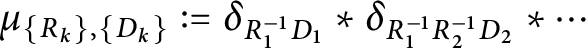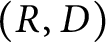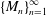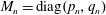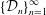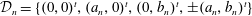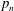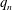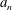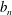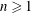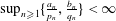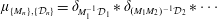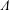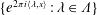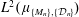Let 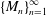 $\{M_{n}\}_{n=1}^{\infty }$ be a sequence of expanding matrices with
$\{M_{n}\}_{n=1}^{\infty }$ be a sequence of expanding matrices with 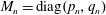 $M_{n}=\operatorname{diag}(p_{n},q_{n})$, and let
$M_{n}=\operatorname{diag}(p_{n},q_{n})$, and let 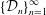 $\{{\mathcal{D}}_{n}\}_{n=1}^{\infty }$ be a sequence of digit sets with
$\{{\mathcal{D}}_{n}\}_{n=1}^{\infty }$ be a sequence of digit sets with 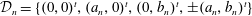 ${\mathcal{D}}_{n}=\{(0,0)^{t},(a_{n},0)^{t},(0,b_{n})^{t},\pm (a_{n},b_{n})^{t}\}$, where
${\mathcal{D}}_{n}=\{(0,0)^{t},(a_{n},0)^{t},(0,b_{n})^{t},\pm (a_{n},b_{n})^{t}\}$, where 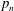 $p_{n}$,
$p_{n}$, 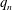 $q_{n}$,
$q_{n}$, 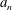 $a_{n}$ and
$a_{n}$ and 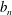 $b_{n}$ are positive integers for all
$b_{n}$ are positive integers for all 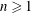 $n\geqslant 1$. If
$n\geqslant 1$. If 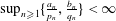 $\sup _{n\geqslant 1}\{\frac{a_{n}}{p_{n}},\frac{b_{n}}{q_{n}}\}<\infty$, then the infinite convolution
$\sup _{n\geqslant 1}\{\frac{a_{n}}{p_{n}},\frac{b_{n}}{q_{n}}\}<\infty$, then the infinite convolution 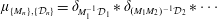 $\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}}=\unicode[STIX]{x1D6FF}_{M_{1}^{-1}{\mathcal{D}}_{1}}\ast \unicode[STIX]{x1D6FF}_{(M_{1}M_{2})^{-1}{\mathcal{D}}_{2}}\ast \cdots \,$ is a Borel probability measure (Cantor–Dust–Moran measure). In this paper, we investigate whenever there exists a discrete set
$\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}}=\unicode[STIX]{x1D6FF}_{M_{1}^{-1}{\mathcal{D}}_{1}}\ast \unicode[STIX]{x1D6FF}_{(M_{1}M_{2})^{-1}{\mathcal{D}}_{2}}\ast \cdots \,$ is a Borel probability measure (Cantor–Dust–Moran measure). In this paper, we investigate whenever there exists a discrete set 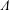 $\unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6EC}$ such that 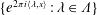 $\{e^{2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D706},x\rangle }:\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}\}$ is an orthonormal basis for
$\{e^{2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D706},x\rangle }:\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}\}$ is an orthonormal basis for 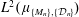 $L^{2}(\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}})$.
$L^{2}(\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}})$.
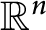 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets