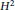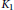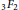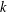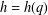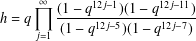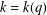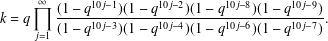Refine search
Actions for selected content:
13 results
ON A WEIGHTED SUM OF MULTIPLE $\mathbf{{T}}$
 -VALUES OF FIXED WEIGHT AND DEPTH
-VALUES OF FIXED WEIGHT AND DEPTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 398-405
- Print publication:
- December 2021
-
- Article
- Export citation
8 - Jacobi Polynomials and Hypergeometric Functions Associated with Root Systems
-
-
- Book:
- Encyclopedia of Special Functions: The Askey-Bateman Project
- Published online:
- 30 September 2020
- Print publication:
- 15 October 2020, pp 217-257
-
- Chapter
- Export citation
Hypergeometric rational approximations to ζ(4)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 374-397
-
- Article
-
- You have access
- Open access
- Export citation
CM Periods, CM Regulators, and Hypergeometric Functions, I
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 3 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-514
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
On the Mabinogion urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 327-346
- Print publication:
- June 2018
-
- Article
- Export citation
ON THE EVALUATION OF MULTIVARIATE COMPOUND DISTRIBUTIONS WITH CONTINUOUS SEVERITY DISTRIBUTIONS AND SARMANOV'S COUNTING DISTRIBUTION
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 48 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 17 January 2018, pp. 841-870
- Print publication:
- May 2018
-
- Article
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
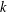 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
RANDOM WALKS, ELLIPTIC INTEGRALS AND RELATED CONSTANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 166-167
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
NOTE ON A HYPERGEOMETRIC INTEGRAL
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 3 / October 2007
- Published online by Cambridge University Press:
- 08 January 2008, pp. 701-710
-
- Article
-
- You have access
- Export citation
Coalescent lineage distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 405-429
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
An alternating motion with stops and the related planar, cyclic motion with four directions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1153-1168
- Print publication:
- December 2003
-
- Article
- Export citation
Duality for hypergeometric functions and invariant Gauss-Manin systems
-
- Journal:
- Compositio Mathematica / Volume 108 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 77-106
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation