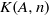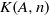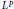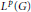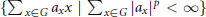Refine search
Actions for selected content:
15 results
5 - From Spin-1/2 Cluster c Chains to Majorana c Chains
-
- Book:
- Fractionalization of Particles in Physics
- Published online:
- 09 January 2025
- Print publication:
- 23 January 2025, pp 303-418
-
- Chapter
- Export citation
Four-fold Massey products in Galois cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 1921-1959
- Print publication:
- September 2018
-
- Article
- Export citation
AN EXPLICIT DESCRIPTION OF THE SIMPLICIAL GROUP
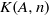 $K(A, n)$
$K(A, n)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 133-144
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Hermitian periodicity and cohomology of infinite orthogonal groups
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 23 May 2013, pp. 203-211
- Print publication:
- August 2013
-
- Article
- Export citation
Quillen's work on the Adams Conjecture
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 11 March 2013, pp. 517-526
- Print publication:
- June 2013
-
- Article
- Export citation
Nilpotence in group cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 151-175
-
- Article
-
- You have access
- Export citation
On the conjectural Leibniz cohomology for groups
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 30 November 2012, pp. 519-563
- Print publication:
- December 2012
-
- Article
- Export citation
The braided monoidal structures on the category of vector spaces graded by the Klein group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 613-641
-
- Article
-
- You have access
- Export citation
Group cohomology with coefficients in a crossed module
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 17 June 2010, pp. 359-404
- Print publication:
- April 2011
-
- Article
- Export citation
Homology of some Artin and twisted Artin Groups
-
- Journal:
- Journal of K-Theory / Volume 6 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2009, pp. 171-196
- Print publication:
- August 2010
-
- Article
- Export citation
JACOBI-LIKE FORMS, PSEUDODIFFERENTIAL OPERATORS, AND GROUP COHOMOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 55-71
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Homotopy Formulas for Cyclic Groups Acting on Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
Group Cohomology and
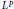 ${{L}^{p}}$ -Cohomology of Finitely Generated Groups
${{L}^{p}}$ -Cohomology of Finitely Generated Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 2 / 01 June 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 268-276
- Print publication:
- 01 June 2003
-
- Article
-
- You have access
- Export citation
THE EULER CLASS OF A POINCARÉ DUALITY GROUP
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 17 June 2002, pp. 421-448
-
- Article
-
- You have access
- Export citation
THE SUBRING OF GROUP COHOMOLOGY CONSTRUCTED BY PERMUTATION REPRESENTATIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 05 February 2002, pp. 241-253
-
- Article
-
- You have access
- Export citation