No CrossRef data available.
Article contents
AN EXPLICIT DESCRIPTION OF THE SIMPLICIAL GROUP  $K(A, n)$
$K(A, n)$
Published online by Cambridge University Press: 07 June 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We give an explicit construction for a 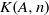 $K(A, n)$ simplicial group and explain its topological interpretation.
$K(A, n)$ simplicial group and explain its topological interpretation.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Connes, A. and Moscovici, H., ‘Cyclic cohomology and Hopf algebras’, Lett. Math. Phys. 48 (1) (1999), 97–108.CrossRefGoogle Scholar
Crainic, M., ‘Cyclic cohomology of Hopf algebras’, J. Pure Appl. Algebra 166 (1) (2002), 29–66.CrossRefGoogle Scholar
Eilenberg, S. and MacLane, S., ‘Determination of the second homology and cohomology groups of a space by means of homotopy invariants’, Proc. Nat. Acad. Sci. USA 32 (1946), 277–280.CrossRefGoogle ScholarPubMed
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics, 174 (Birkhäuser, Basel, 1999).CrossRefGoogle Scholar
Khalkhali, M. and Rangipour, B., ‘A new cyclic module for Hopf algebras’, K-Theory 27 (2002), 111–131.CrossRefGoogle Scholar
Loday, J. L., Cyclic Homology, Grundlehren der Mathematischen Wissenschaften, 301 (Springer, Berlin, 1992).CrossRefGoogle Scholar
May, J. P., Simplicial Objects in Algebraic Topology, Chicago Lectures in Mathematics (1967).Google Scholar
Staic, M. D., ‘Secondary cohomology and k-invariants’, Bull. Belg. Math. Soc. 19 (3) (2012), 561–572.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics (1995).Google Scholar

