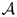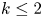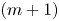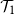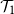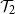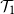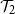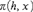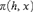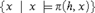4 results
A Lebesgue–Lusin property for linear operators of first and second order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-11
-
- Article
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
COMPONENTS AND MINIMAL NORMAL SUBGROUPS OF FINITE AND PSEUDOFINITE GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 14 March 2019, pp. 290-300
- Print publication:
- March 2019
-
- Article
- Export citation
ASPeRiX, a first-order forward chaining approach for answer set computing*
-
- Journal:
- Theory and Practice of Logic Programming / Volume 17 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 266-310
-
- Article
- Export citation