Refine search
Actions for selected content:
11 results
II - Foundations
-
- Book:
- Albert Algebras over Commutative Rings
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 43-108
-
- Chapter
- Export citation
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 256-262
- Print publication:
- October 2021
-
- Article
- Export citation
HECKE ALGEBRAS FOR INNER FORMS OF
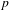 $p$ -ADIC SPECIAL LINEAR GROUPS
$p$ -ADIC SPECIAL LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 May 2015, pp. 351-419
- Print publication:
- April 2017
-
- Article
- Export citation
On the motive of the group of units of a division algebra
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 17 March 2014, pp. 533-561
- Print publication:
- June 2014
-
- Article
- Export citation
Extension du formalisme de Bushnell et Kutzko aucas d'une algèbre à division
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 77 / Issue 2 / September 1998
- Published online by Cambridge University Press:
- 01 September 1998, pp. 292-326
- Print publication:
- September 1998
-
- Article
- Export citation
Reduced Norm Map of Division Algebras over Complete Discrete Valuation Fields of Certain Type
-
- Journal:
- Compositio Mathematica / Volume 112 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 04 December 2007, pp. 127-145
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Reduced Norm Map of Division Algebras over Complete Discrete Valuation Fields of Certain Type
-
- Journal:
- Compositio Mathematica / Volume 112 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 04 December 2007, pp. 127-145
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Division Graded Algebras in the Brauer-Wall Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 1 / 01 March 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-24
- Print publication:
- 01 March 1996
-
- Article
-
- You have access
- Export citation
Banach Algebras Which are a Direct Sum of Division Algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-145
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
Preservation of elementary equivalence under scalar extension1
-
- Journal:
- The Journal of Symbolic Logic / Volume 47 / Issue 4 / December 1982
- Published online by Cambridge University Press:
- 12 March 2014, pp. 734-738
- Print publication:
- December 1982
-
- Article
- Export citation
Cyclotomic Splitting Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 2 / 01 June 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-229
- Print publication:
- 01 June 1982
-
- Article
-
- You have access
- Export citation
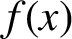
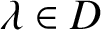
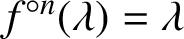
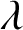
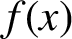
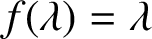


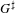

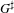
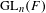
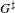
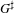
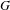
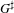

 (
(