Article contents
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
Published online by Cambridge University Press: 01 March 2021
Abstract
We study the discrete dynamics of standard (or left) polynomials 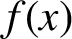 $f(x)$ over division rings D. We define their fixed points to be the points
$f(x)$ over division rings D. We define their fixed points to be the points 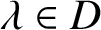 $\lambda \in D$ for which
$\lambda \in D$ for which 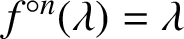 $f^{\circ n}(\lambda )=\lambda $ for any
$f^{\circ n}(\lambda )=\lambda $ for any 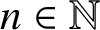 $n \in \mathbb {N}$, where
$n \in \mathbb {N}$, where 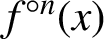 $f^{\circ n}(x)$ is defined recursively by
$f^{\circ n}(x)$ is defined recursively by 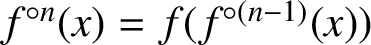 $f^{\circ n}(x)=f(f^{\circ (n-1)}(x))$ and
$f^{\circ n}(x)=f(f^{\circ (n-1)}(x))$ and 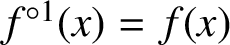 $f^{\circ 1}(x)=f(x)$. Periodic points are similarly defined. We prove that
$f^{\circ 1}(x)=f(x)$. Periodic points are similarly defined. We prove that 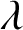 $\lambda $ is a fixed point of
$\lambda $ is a fixed point of 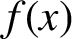 $f(x)$ if and only if
$f(x)$ if and only if 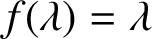 $f(\lambda )=\lambda $, which enables the use of known results from the theory of polynomial equations, to conclude that any polynomial of degree
$f(\lambda )=\lambda $, which enables the use of known results from the theory of polynomial equations, to conclude that any polynomial of degree 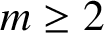 $m \geq 2$ has at most m conjugacy classes of fixed points. We also show that in general, periodic points do not behave as in the commutative case. We provide a sufficient condition for periodic points to behave as expected.
$m \geq 2$ has at most m conjugacy classes of fixed points. We also show that in general, periodic points do not behave as in the commutative case. We provide a sufficient condition for periodic points to behave as expected.
Keywords
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 256 - 262
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
The first author acknowledges the receipt of the Chateaubriand Fellowship (969845L) offered by the French Embassy in Israel.
References
- 3
- Cited by


