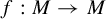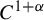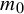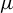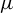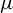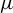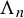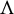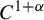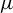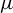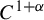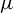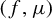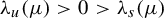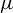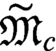Refine search
Actions for selected content:
36 results
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
Shared differential factors underlying individual spontaneous neural activity abnormalities in major depressive disorder
-
- Journal:
- Psychological Medicine / Volume 54 / Issue 15 / November 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 4316-4334
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Subspaces, Rank, and Nearest-Subspace Classification
-
- Book:
- Linear Algebra for Data Science, Machine Learning, and Signal Processing
- Published online:
- 01 November 2024
- Print publication:
- 16 May 2024, pp 96-142
-
- Chapter
- Export citation
Dimension in team semantics
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 410-454
-
- Article
- Export citation
Dimension estimates and approximation in non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 2975-3001
- Print publication:
- October 2024
-
- Article
- Export citation
The future of diagnosis in clinical neurosciences: Comparing multiple sclerosis and schizophrenia
- Part of
-
- Journal:
- European Psychiatry / Volume 66 / Issue 1 / 2023
- Published online by Cambridge University Press:
- 21 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Bases and Similarity
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 26-55
-
- Chapter
- Export citation
Dimension approximation in smooth dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 383-407
- Print publication:
- February 2024
-
- Article
- Export citation
6 - Vector Spaces
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 126-148
-
- Chapter
- Export citation
Radiological dimensions of the Eustachian tube in patients with adhesive otitis media
-
- Journal:
- The Journal of Laryngology & Otology / Volume 137 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 520-523
- Print publication:
- May 2023
-
- Article
- Export citation
9 - Figures and Tables
-
- Book:
- Scientific Writing and Publishing
- Published online:
- 14 October 2021
- Print publication:
- 30 September 2021, pp 111-126
-
- Chapter
- Export citation
Towards a contemporary approach for understanding personality pathology in developmental context: An integrative model
-
- Journal:
- Development and Psychopathology / Volume 33 / Issue 5 / December 2021
- Published online by Cambridge University Press:
- 27 July 2021, pp. 1793-1802
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
D - Fractal Dimension
- from Appendices
-
- Book:
- Modern Classical Mechanics
- Published online:
- 30 November 2020
- Print publication:
- 10 December 2020, pp 674-675
-
- Chapter
- Export citation
C - Dimensional Reasoning
- from Appendices
-
- Book:
- Modern Classical Mechanics
- Published online:
- 30 November 2020
- Print publication:
- 10 December 2020, pp 670-673
-
- Chapter
- Export citation
8 - Time and Space: The Implicit Measure of Motion in Aristotle’s Physics
-
- Book:
- The Concept of Motion in Ancient Greek Thought
- Published online:
- 28 September 2020
- Print publication:
- 08 October 2020, pp 335-384
-
- Chapter
- Export citation
DIMENSIONAL GROUPS AND FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 918-936
- Print publication:
- September 2020
-
- Article
- Export citation
Dimensions over categories: a meta-analysis of taxometric research
-
- Journal:
- Psychological Medicine / Volume 50 / Issue 9 / July 2020
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1418-1432
-
- Article
- Export citation
The relationship between predisposing factors, premorbid function and symptom dimensions in psychosis: an integrated approach
-
- Journal:
- European Psychiatry / Volume 17 / Issue 6 / October 2002
- Published online by Cambridge University Press:
- 16 April 2020, pp. 311-320
-
- Article
- Export citation
Affective dimensions as a diagnostic tool for bipolar disorder in first psychotic episodes
-
- Journal:
- European Psychiatry / Volume 29 / Issue 7 / September 2014
- Published online by Cambridge University Press:
- 15 April 2020, pp. 424-430
-
- Article
- Export citation

Geometric Regular Polytopes
-
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020