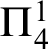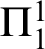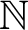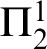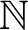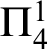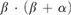The Kruskal–Friedman theorem asserts: in any infinite sequence of finite trees with ordinal labels, some tree can be embedded into a later one, by an embedding that respects a certain gap condition. This strengthening of the original Kruskal theorem has been proved by I. Kříž (Ann. Math. 1989), in confirmation of a conjecture due to H. Friedman, who had established the result for finitely many labels. It provides one of the strongest mathematical examples for the independence phenomenon from Gödel’s theorems. The gap condition is particularly relevant due to its connection with the graph minor theorem of N. Robertson and P. Seymour. In the present article, we consider a uniform version of the Kruskal–Friedman theorem, which extends the result from trees to general recursive data types. Our main theorem shows that this uniform version is equivalent both to  $\Pi ^1_1$-transfinite recursion and to a minimal bad sequence principle of Kříž, over the base theory
$\Pi ^1_1$-transfinite recursion and to a minimal bad sequence principle of Kříž, over the base theory  $\mathsf {RCA_0}$ from reverse mathematics. This sheds new light on the role of infinity in finite combinatorics.
$\mathsf {RCA_0}$ from reverse mathematics. This sheds new light on the role of infinity in finite combinatorics.
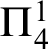 ${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY