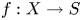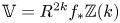Refine search
Actions for selected content:
6 results
Non-agreeing degree constructions
-
- Journal:
- Journal of Linguistics / Volume 61 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 04 June 2024, pp. 265-300
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Mystical Experience
-
- Book:
- Ways of Living Religion
- Published online:
- 07 March 2024
- Print publication:
- 14 March 2024, pp 131-179
-
- Chapter
- Export citation
Sets of special subvarieties of bounded degree
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 14 March 2023, pp. 616-657
- Print publication:
- March 2023
-
- Article
- Export citation
9 - A Typology of Semantic Entities
- from Part V - Typologizing and Ontologizing
-
-
- Book:
- Linguistics Meets Philosophy
- Published online:
- 06 October 2022
- Print publication:
- 13 October 2022, pp 277-301
-
- Chapter
- Export citation
Participation and Degrees
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beliefs do not come in degrees
-
- Journal:
- Canadian Journal of Philosophy / Volume 47 / Issue 6 / 2017
- Published online by Cambridge University Press:
- 01 January 2020, pp. 760-778
-
- Article
- Export citation