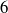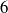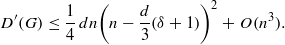Let G be a finite connected graph of order n, minimum degree δ and diameter d. The degree distance D′(G) of G is defined as ∑ {u,v}⊆V (G)(deg u+deg v) d(u,v), where deg w is the degree of vertex w and d(u,v)denotes the distance between u and v. In this paper, we find an asymptotically sharp upper bound on the degree distance in terms of order, minimum degree and diameter. In particular, we prove that 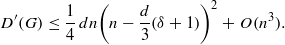 \[ D^\prime (G)\le \frac {1}{4}\,dn\biggl (n-\frac {d}{3}(\delta +1)\biggr )^2+O(n^3). \]
\[ D^\prime (G)\le \frac {1}{4}\,dn\biggl (n-\frac {d}{3}(\delta +1)\biggr )^2+O(n^3). \]
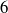 $6$
$6$