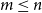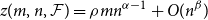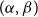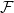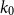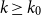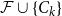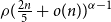Refine search
Actions for selected content:
37 results
28 - Generative Accounts of Change
- from Part IV - Modelling the Record: Methods and Theories
-
-
- Book:
- The New Cambridge History of the English Language
- Published online:
- 18 October 2025
- Print publication:
- 16 October 2025, pp 694-717
-
- Chapter
- Export citation
Financial complexity, cycles and income inequality
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e141
-
- Article
- Export citation
8 - Spatio-temporal Analysis
-
- Book:
- Spatial Analysis
- Published online:
- 19 June 2025
- Print publication:
- 03 July 2025, pp 227-257
-
- Chapter
- Export citation
Insurance cycles detection using neural networks
-
- Journal:
- Annals of Actuarial Science / Volume 19 / Issue 2 / July 2025
- Published online by Cambridge University Press:
- 09 May 2025, pp. 350-371
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Spectral Analysis
-
- Book:
- Time Series for Economics and Finance
- Published online:
- 19 December 2024
- Print publication:
- 19 December 2024, pp 102-128
-
- Chapter
- Export citation
Comparisons of Structural Fe Reduction in Smectites by Bacteria and Dithionite: An Infrared Spectroscopic Study
-
- Journal:
- Clays and Clay Minerals / Volume 54 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 01 January 2024, pp. 195-208
-
- Article
- Export citation
On oriented cycles in randomly perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 157-178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bipartite-ness under smooth conditions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 546-558
-
- Article
- Export citation
Intransitive preferences or choice errors? A reply to Birnbaum
-
- Journal:
- Judgment and Decision Making / Volume 15 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 01 January 2023, pp. 1052-1053
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Predictably intransitive preferences
-
- Journal:
- Judgment and Decision Making / Volume 13 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 01 January 2023, pp. 217-236
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Movements in Revolutionary Cycles
- from Part III - Dynamics of Contention
-
- Book:
- Power in Movement
- Published online:
- 25 August 2022
- Print publication:
- 11 August 2022, pp 211-233
-
- Chapter
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1031-1047
-
- Article
- Export citation
Chapter 11 - Dissecting the Psychology of a Voter
- from Part II - By the People
-
-
- Book:
- Psychology of Democracy
- Published online:
- 24 February 2022
- Print publication:
- 03 March 2022, pp 250-264
-
- Chapter
- Export citation
5 - Chaconnes in the Music of Adès
-
-
- Book:
- Thomas Adès Studies
- Published online:
- 18 November 2021
- Print publication:
- 25 November 2021, pp 93-116
-
- Chapter
- Export citation

The Dynamics of Public Opinion
-
- Published online:
- 20 September 2021
- Print publication:
- 11 November 2021
-
- Element
- Export citation
15 - Romantic Forms
- from Part IV - Practices
-
-
- Book:
- The Cambridge Companion to Music and Romanticism
- Published online:
- 06 August 2021
- Print publication:
- 26 August 2021, pp 258-276
-
- Chapter
- Export citation
Most permutations power to a cycle of small prime length
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 24 May 2021, pp. 234-246
-
- Article
- Export citation
4 - Expanders – how to find them, and what to find in them
-
-
- Book:
- Surveys in Combinatorics 2019
- Published online:
- 17 June 2019
- Print publication:
- 27 June 2019, pp 115-142
-
- Chapter
- Export citation
EXTENDING THE DOUBLE RAMIFICATION CYCLE BY RESOLVING THE ABEL-JACOBI MAP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 May 2019, pp. 331-359
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation