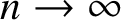Refine search
Actions for selected content:
1 results
Topology of random
 $2$-dimensional cubical complexes
$2$-dimensional cubical complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation