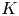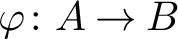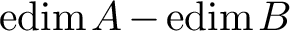Refine search
Actions for selected content:
15 results
Delta-invariants of complete intersection log del Pezzo surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 1021-1036
- Print publication:
- June 2023
-
- Article
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A weak Lefschetz result for Chow groups of complete intersections
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1014-1023
- Print publication:
- December 2021
-
- Article
- Export citation
Degrees of Regular Sequences With a Symmetric Group Action
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 557-578
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Finite Determinacy and Stability of Flatnessof Analytic Mappings
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-257
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
Some Homological Criteria for Regular, Complete Intersection and Gorenstein Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 473-481
-
- Article
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES – CORRIGENDUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 August 2014, p. 751
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 05 June 2014, pp. 703-749
- Print publication:
- October 2015
-
- Article
- Export citation
Subcategories of singularity categories via tensor actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 22 November 2013, pp. 229-272
- Print publication:
- February 2014
-
- Article
- Export citation
Normality of Maximal Orbit Closures for Euclidean Quivers
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 6 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1222-1247
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
A generalized Gaeta’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 689-704
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
The unirationality of the moduli spaces of curves of genus 14 or lower
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1425-1444
- Print publication:
- November 2005
-
- Article
-
- You have access
- Export citation
Monomial Ideals and the Gorenstein Liaison Class of a Complete Intersection
-
- Journal:
- Compositio Mathematica / Volume 133 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 25-36
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Transformée de Mellin des intégrales-fibres associées aux singularités isolées d'intersection complète quasihomogènes. (Mellin Transform of Fibre Integrals Associated to Isolated Complete Intersection Singularities)
-
- Journal:
- Compositio Mathematica / Volume 130 / Issue 2 / January 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 119-160
- Print publication:
- January 2002
-
- Article
-
- You have access
- Export citation
Some Properties of Finite Morphisms on Double Points
-
- Journal:
- Compositio Mathematica / Volume 121 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 35-53
- Print publication:
- March 2000
-
- Article
-
- You have access
- Export citation