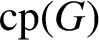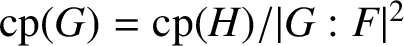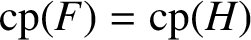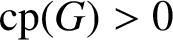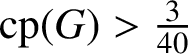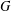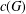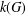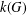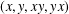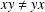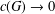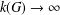Refine search
Actions for selected content:
3 results
COMMUTING PROBABILITY OF COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 June 2021, pp. 87-91
- Print publication:
- February 2022
-
- Article
- Export citation
SCHUR’S COLOURING THEOREM FOR NONCOMMUTING PAIRS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 446-452
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Commutativity preserving extensions of groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 575-592
- Print publication:
- June 2018
-
- Article
- Export citation